设a＞0 为建立求设χ*是方程f(χ)＝0的一个根 f(χ)在χ*的某邻域内三次连续可微 且f(χ*
设a＞0，为建立求设χ*是方程f(χ)＝0的一个根，f(χ)在χ*的某邻域内三次连续可微，且f(χ*)≠0，对Newton法
设χ*是方程f(χ)＝0的一个根，f(χ)在χ*的某邻域内三次连续可微，且f(χ*)≠0，对Newton法做如下修正： 
它称为单点Steffensen方法。证明：单点Steffensen方法是二阶收敛法，并用此格式计算
。
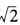请帮忙给出正确答案和分析，谢谢！
参考解答
4j8***102
2024-11-17 07:07:34
正确答案：因χ*是方程f(χ)＝0的根且f′(χ*)≠0故可设f(χ)＝(χ－χ*)h(χ)其中h(χ*)≠0记en＝χn－χ*只要证明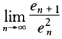
＝c(c为非零常数)即可。
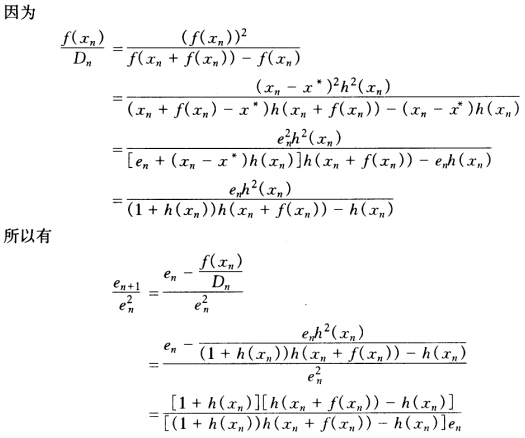对等式两边取极限有
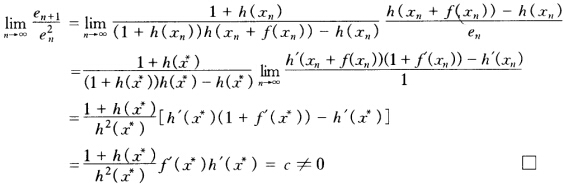所以单点Steffenson迭代格式具有二阶收敛。 
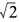≈χ6＝1．4142135624。
因χ*是方程f(χ)＝0的根,且f′(χ*)≠0,故可设f(χ)＝(χ－χ*),h(χ),其中h(χ*)≠0,记en＝χn－χ*,只要证明＝c(c为非零常数)即可。对等式两边取极限有所以单点Steffenson迭代格式具有二阶收敛。≈χ6＝1．4142135624。
相似问题
用平面旋转变换和反射变换将向量x=(2 3 0 5)T变为与单位向量e1=(1 0 0 0)T平行的
用平面旋转变换和反射变换将向量x=(2，3，0，5)T变为与单位向量e1=(1，0，0，0)T平行的向量．请帮忙给出正确答案和分析，谢谢！
已知函数y＝(χ)过点(1 0) (2 －5) (3 －6) (4 3) 求经过这些点的Lagran
已知函数y＝(χ)过点(1，0)，(2，－5)，(3，－6)，(4，3)，求经过这些点的Lagrange插值多项式L3(χ)，并求f(已已知当χ＝－1，0，2，3时，对应的函数值为
试用n＝1 2 3 4的Newton－cotes求积公式计算定积分I＝设f(χ)∈C[a b] 证明
试用n＝1，2，3，4的Newton－cotes求积公式计算定积分I＝设f(χ)∈C[a，b]，证明：复化梯形求积公式和复化Si设f(χ)∈C[a，b]，证明：复化梯形求积公式和
已知函数y＝(χ)过点(1 0) (2 －5) (3 －6) (4 3) 求经过这些点的Lagran
已知函数y＝(χ)过点(1，0)，(2，－5)，(3，－6)，(4，3)，求经过这些点的Lagrange插值多项式L3(χ)，并求f(设χ设χ0≠χ2，证明有唯一的三次多项式P(χ
设A是对称正定矩阵 证明：是向量χ的范数。请帮忙给出正确答案和分析 谢谢！
设A是对称正定矩阵，证明：是向量χ的范数。请帮忙给出正确答案和分析，谢谢！
