用平面旋转变换和反射变换将向量x=(2 3 0 5)T变为与单位向量e1=(1 0 0 0)T平行的

参考解答

406***102

2024-11-17 07:10:08



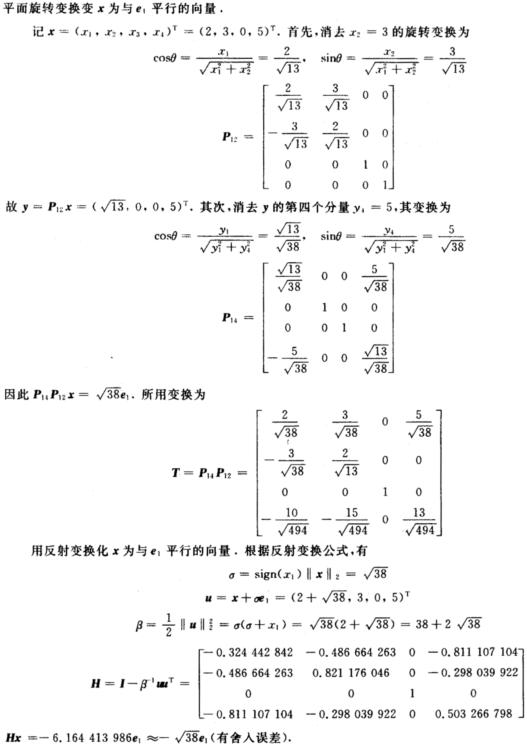
相似问题

• 已知函数y＝(χ)过点(1 0) (2 －5) (3 －6) (4 3) 求经过这些点的Lagran

  已知函数y＝(χ)过点(1，0)，(2，－5)，(3，－6)，(4，3)，求经过这些点的Lagrange插值多项式L3(χ)，并求f(已已知当χ＝－1，0，2，3时，对应的函数值为

• 试用n＝1 2 3 4的Newton－cotes求积公式计算定积分I＝设f(χ)∈C[a b] 证明

  试用n＝1，2，3，4的Newton－cotes求积公式计算定积分I＝设f(χ)∈C[a，b]，证明：复化梯形求积公式和复化Si设f(χ)∈C[a，b]，证明：复化梯形求积公式和

• 已知函数y＝(χ)过点(1 0) (2 －5) (3 －6) (4 3) 求经过这些点的Lagran

  已知函数y＝(χ)过点(1，0)，(2，－5)，(3，－6)，(4，3)，求经过这些点的Lagrange插值多项式L3(χ)，并求f(设χ设χ0≠χ2，证明有唯一的三次多项式P(χ

• 设A是对称正定矩阵 证明：是向量χ的范数。请帮忙给出正确答案和分析 谢谢！

  设A是对称正定矩阵，证明：是向量χ的范数。请帮忙给出正确答案和分析，谢谢！

• 已知函数y＝(χ)过点(1 0) (2 －5) (3 －6) (4 3) 求经过这些点的Lagran

  已知函数y＝(χ)过点(1，0)，(2，－5)，(3，－6)，(4，3)，求经过这些点的Lagrange插值多项式L3(χ)，并求f(设设函数f(χ)＝，假设我们在χ0＝1，χ1＝2