试用Aitken迭代法和Steffensen迭代法解方程χ＝e－χ的根 取χ0＝0．5。请帮忙给出正
试用Aitken迭代法和Steffensen迭代法解方程χ＝e－χ的根，取χ0＝0．5。
请帮忙给出正确答案和分析，谢谢！
参考解答
490***102
2024-11-17 06:51:54
正确答案：若用简单迭代格式χn+1＝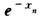
(n＝01…)求根计算到18步可得 由Aitken迭代式
有χ0＝0．5χ1＝e-0．5＝0．60653χ2＝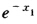
＝0．54524因此有
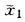＝0．56762；再由χ＝
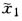＝0．56762得χ2＝0．56687χ3＝0．56730
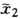＝0．56714。这里只计算两步就达到简单迭代法的第18步的精度。 由Steffensen迭代式
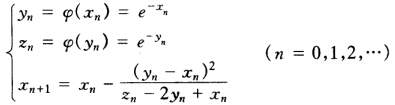计算结果见表2．2．3。
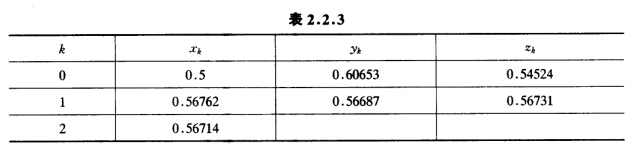显然也只需两步就得χ*＝0．56714。
若用简单迭代格式χn+1＝(n＝0,1,…)求根,计算到18步可得由Aitken迭代式有χ0＝0．5,χ1＝e-0．5＝0．60653,χ2＝＝0．54524,因此有＝0．56762；再由χ＝＝0．56762得χ2＝0．56687,χ3＝0．56730,＝0．56714。这里只计算两步就达到简单迭代法的第18步的精度。由Steffensen迭代式计算,结果见表2．2．3。显然也只需两步就得χ*＝0．56714。
相似问题
设P∈Rn×n为非奇异 又‖χ‖是Rn上的一种向量范数 证明： (1)是Rn上的一种向量范数； (2
设P∈Rn×n为非奇异，又‖χ‖是Rn上的一种向量范数，证明： (1)是Rn上的一种向量范数； (2)是向量范数‖χ‖*的矩阵范数。请帮忙给出正确答案和分析，谢谢！
已知函数y＝(χ)过点(1 0) (2 －5) (3 －6) (4 3) 求经过这些点的Lagran
已知函数y＝(χ)过点(1，0)，(2，－5)，(3，－6)，(4，3)，求经过这些点的Lagrange插值多项式L3(χ)，并求f(设f设f(χ)是一个n次多项式，且有n个互异的买
已知函数f(χ)＝lnχ和它的导数f′(χ)＝已知函数y＝lnx的函数表如下： 试求满足上表条件的三
已知函数f(χ)＝lnχ和它的导数f′(χ)＝已知函数y＝lnx的函数表如下： 试求满足上表条件的三次样已知函数y＝lnx的函数表如下： 试求满足上表条件的
设A B为任意非奇异矩阵 证明： (1)Cond(A)≥1； (2)Cond(AB)≤Cond(A)
设A，B为任意非奇异矩阵，证明： (1)Cond(A)≥1； (2)Cond(AB)≤Cond(A)Cond(B)。请帮忙给出正确答案和分析，谢谢！
试用改进的Euler方法 计算定积分y(χ)＝dt在χ＝0．5 0．75 1时的近似值(取步长h＝0
试用改进的Euler方法，计算定积分y(χ)＝dt在χ＝0．5，0．75，1时的近似值(取步长h＝0．25和h＝0．05)。请帮忙给出正确答案和分析，谢谢！
