用Lagrange方法求解下列问题:min [*]-x1x2+x22-x2x3+[*]+x1+x2+
用Lagrange方法求解下列问题:min [*]-x1x2+x22-x2x3+[*]+x1+x2+x3 s.t. x1+2x2+x3=4.
min [*]-x1x2+x22-x2x3+[*]+x1+x2+x3 s.t. x1+2x2+x3=4.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:定义Lagrange函数L(xλ)=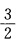 x12一x1x2+x22—x2x3+
x12一x1x2+x22—x2x3+ x32+x1+x2+x3一λ(x1+2x2+x3一4)令
x32+x1+x2+x3一λ(x1+2x2+x3一4)令
定义Lagrange函数L(x,λ)=x12一x1x2+x22—x2x3+x32+x1+x2+x3一λ(x1+2x2+x3一4),令
相似问题
考虑下列问题: min x12+x1x2+2x22一6x1—2x2—12x3 s.t. x1+x2+
考虑下列问题: min x12+x1x2+2x22一6x1—2x2—12x3 s.t. x1+x2+x3=2, 一x1+2x2 ≤3, x1,x2,x3≥0. 求出在点=(1,1,0)T处的一个下降可行
min x12+x1x2+2x22一6x1—2x2—12x3 s.t. x1+x2+x3=2 x1
min x12+x1x2+2x22一6x1—2x2—12x3 s.t. x1+x2+x3=2, x1一2x2 ≥一3, x1,x2,x3≥0, 取初始点x(1)=(1,0,1)T请帮忙给出正确答案和分析,谢谢!
考虑下列问题: 设f(x)=xTAx—bTx A是对称正定矩阵.用最速下降法求f(x)的极小点 迭代
考虑下列问题: 设f(x)=xTAx—bTx,A是对称正定矩阵.用最速下降法求f(x)的极小点,迭代公式如下: 设f(x)=xTAx—bTx,A是对称正定矩阵.用最速下降法
分别用逆推解法及顺推解法min x1+x22+2x3 s.t. x1+x2+x3≥10 x1 x2
分别用逆推解法及顺推解法min x1+x22+2x3 s.t. x1+x2+x3≥10, x1,x2,x3≥0;请帮忙给出正确答案和分析,谢谢!
给定非线性规划问题 max bTx x∈Rn s.t. xTx≤1 其中b≠0.证明向量=b/∥
给定非线性规划问题 max bTx, x∈Rn s.t. xTx≤1, 其中b≠0.证明向量=b/∥b∥满足最优性的充分条件.请帮忙给出正确答案和分析,谢谢!












