求证：级数在｜z｜≥1上发散；在｜z｜＜1内绝对级敛且内闭一致收敛 但非一致收敛．请帮忙给出正确答案
求证：级数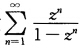
在｜z｜≥1上发散；在｜z｜＜1内绝对级敛且内闭一致收敛，但非一致收敛．
请帮忙给出正确答案和分析，谢谢！
参考解答
481***103
2024-11-21 11:02:37
正确答案：(1)因为当｜z｜≥1时有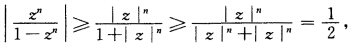
所以当｜z｜≥1时级数发散．(2)设｜z｜≤ρ＜1则存在正整数N当n＞N时｜z｜n≤ρn＜
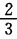从而
(3)级数在｜z｜＜1内非一致收敛．事实上在｜z｜＜1内存在一个点列zn=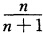
(从比1小的正数去接近1)使得
(1)因为当｜z｜≥1时,有所以当｜z｜≥1时,级数发散．(2)设｜z｜≤ρ＜1,则存在正整数N,当n＞N时,｜z｜n≤ρn＜,从而(3)级数在｜z｜＜1内非一致收敛．事实上,在｜z｜＜1内存在一个点列zn=(从比1小的正数去接近1),使得
相似问题
试证 (1)如果=δ绝对收敛 则 ｜δ｜≤｜v1｜—｜v2｜+…+｜vn｜+…． (2)对任一复数z
试证 (1)如果=δ绝对收敛，则 ｜δ｜≤｜v1｜—｜v2｜+…+｜vn｜+…． (2)对任一复数z ｜ez一1｜≤e|z|一1≤｜z｜e|z|． (3)当0＜｜z｜＜1时 请帮
判断下列复级数的敛散性 若收敛指明条件收敛还是绝对收敛． 问在原点解析 在z=(n=1 2 …)处取
判断下列复级数的敛散性，若收敛指明条件收敛还是绝对收敛． 问在原点解析，在z=(n=1，2，…)处取下列问在原点解析，在z=(n=1，2，…)处取下列各组值的
如果在｜z｜＜1内函数f(z)解析 且 请帮忙给出正确答案和分析 谢谢！
如果在｜z｜＜1内函数f(z)解析，且 请帮忙给出正确答案和分析，谢谢！
设f(z)是整函数 n为正整数 试证当 时 f(z)至多是n一1次多项式．请帮忙给出正确答案和分析
设f(z)是整函数，n为正整数，试证当 时，f(z)至多是n一1次多项式．请帮忙给出正确答案和分析，谢谢！
试证试证： (1)cosh2 z—sinh2 z=1； (2)sech2 z＋tanh2 z=1；
试证试证： (1)cosh2 z—sinh2 z=1； (2)sech2 z＋tanh2 z=1； (3)cosh(z1＋z2)=cosh z1cosh z2＋sin试证： (1)cosh2 z—sinh2 z=1； (2)se
