判断下列复级数的敛散性 若收敛指明条件收敛还是绝对收敛． 问在原点解析 在z=(n=1 2 …)处取
判断下列复级数的敛散性，若收敛指明条件收敛还是绝对收敛． 问在原点解析，在z=(n=1，2，…)处取下列
问在原点解析，在z=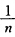
(n=1，2，…)处取下列各组值的函数是否存在?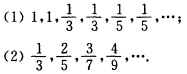 
请帮忙给出正确答案和分析，谢谢！
参考解答
463***103
2024-11-21 10:47:46
正确答案：(1)不存在．事实上若存在函数f(z)在z=0解析且满足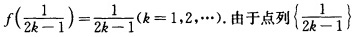
以z=0为极限点故由唯一性定理知f(z)=z(在z=0的邻域内)这与题设
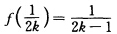矛盾．(2)由于函数的值点列为
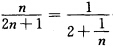(n=12…)故可作函数f(z)=
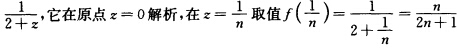(n=一12…)．故所求合题设条件的函数存在就是f(z)=
。
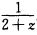(1)不存在．事实上,若存在函数f(z)在z=0解析且满足以z=0为极限点,故由唯一性定理知f(z)=z(在z=0的邻域内),这与题设矛盾．(2)由于函数的值点列为(n=1,2,…),故可作函数f(z)=(n=一1,2,…)．故所求合题设条件的函数存在,就是f(z)=。
相似问题
如果在｜z｜＜1内函数f(z)解析 且 请帮忙给出正确答案和分析 谢谢！
如果在｜z｜＜1内函数f(z)解析，且 请帮忙给出正确答案和分析，谢谢！
设f(z)是整函数 n为正整数 试证当 时 f(z)至多是n一1次多项式．请帮忙给出正确答案和分析
设f(z)是整函数，n为正整数，试证当 时，f(z)至多是n一1次多项式．请帮忙给出正确答案和分析，谢谢！
试证试证： (1)cosh2 z—sinh2 z=1； (2)sech2 z＋tanh2 z=1；
试证试证： (1)cosh2 z—sinh2 z=1； (2)sech2 z＋tanh2 z=1； (3)cosh(z1＋z2)=cosh z1cosh z2＋sin试证： (1)cosh2 z—sinh2 z=1； (2)se
如果将下列函数按z一1的幂展开 并指明其收敛范围：将下列函数按z一1的幂展开 并指明其收敛范围： 请
如果将下列函数按z一1的幂展开，并指明其收敛范围：将下列函数按z一1的幂展开，并指明其收敛范围： 请帮忙给出正确答案和分析，谢谢！
计算：(1)∫－2－2＋i (z＋2) 2dz；(2) ∫0π＋2i cos求积分 ∫02πa(2z
计算：(1)∫－2－2＋i (z＋2) 2dz；(2) ∫0π＋2i cos求积分 ∫02πa(2z2＋8z＋1)dz 之值，其中积分路径是求积分 ∫02πa(2z2+8z+1)dz 之值，其
