计算：(1)∫－2－2＋i (z＋2) 2dz；(2) ∫0π＋2i cos求积分 ∫02πa(2z
计算：(1)∫－2－2＋i (z＋2) 2dz；(2) ∫0π＋2i cos求积分 ∫02πa(2z2＋8z＋1)dz 之值，其中积分路径是
求积分 ∫02πa(2z2+8z+1)dz 之值，其中积分路径是连接0到2πa的摆线： z=a(θ一sinθ)，y=a(1一cosθ)．
请帮忙给出正确答案和分析，谢谢！
参考解答
463***103
2024-11-21 10:24:21
正确答案：由于f(z)=2z2+8z+1在z平面上解析所以在z平面内积分与路径无关． 因此选择最简单的路径为连接0与2πa的直线段[02πa则 r(2z2+8z+1)dz=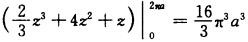
+16π2a2+2πa
由于f(z)=2z2+8z+1在z平面上解析,所以在z平面内积分与路径无关．因此,选择最简单的路径为连接0与2πa的直线段[0,2πa,则r(2z2+8z+1)dz=+16π2a2+2πa
相似问题
设｜zk｜=1(k=1 2 … n)． 试证：请帮忙给出正确答案和分析 谢谢！
设｜zk｜=1(k=1，2，…，n)． 试证：请帮忙给出正确答案和分析，谢谢！
设函数f(z)在z平面上解析 且｜f(z)｜恒大于一个正的常数 试证f(z)必为常数．请帮忙给出正确
设函数f(z)在z平面上解析，且｜f(z)｜恒大于一个正的常数，试证f(z)必为常数．请帮忙给出正确答案和分析，谢谢！
如果设z0是函数f(z)的m阶零点 又是g(z)的n阶零点 试问下列函数在z0处具有何种性质? (1
如果设z0是函数f(z)的m阶零点，又是g(z)的n阶零点，试问下列函数在z0处具有何种性质? (1)f(z)设z0是函数f(z)的m阶零点，又是g(z)的n阶零点，试问下列函
试证试证(sinh z)=cosh z；(cosh z)=sinh z．试证(sinh z)=cos
试证试证(sinh z)=cosh z；(cosh z)=sinh z．试证(sinh z)=cosh z；(cosh z)=sinh z．请帮忙给出正确答案和分析，谢谢！
已知u+v=(x—y)(x2+4xy+y2)一2(x+y) 试确定解析函数f(z)=u+iv．请帮忙
已知u+v=(x—y)(x2+4xy+y2)一2(x+y)，试确定解析函数f(z)=u+iv．请帮忙给出正确答案和分析，谢谢！
