如果在|z|<1内函数f(z)解析 且 请帮忙给出正确答案和分析 谢谢!
如果在|z|<1内函数f(z)解析,且 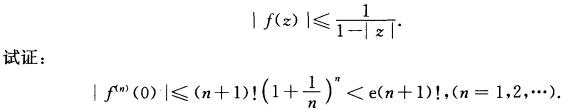
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:取圆周|z|=ρ<1由于f(z)在|z|<1内解析故知f(z)在|z|≤ρ上解析且有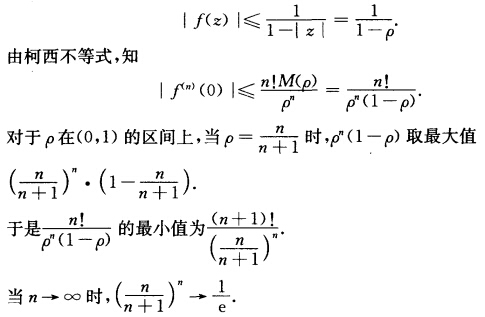 故得|f(n)(0)|的估值为|f(n)(0)|≤(n+1)!e.
故得|f(n)(0)|的估值为|f(n)(0)|≤(n+1)!e.
取圆周|z|=ρ<1由于f(z)在|z|<1内解析,故知f(z)在|z|≤ρ上解析,且有故得|f(n)(0)|的估值为|f(n)(0)|≤(n+1)!e.
相似问题
设f(z)是整函数 n为正整数 试证当 时 f(z)至多是n一1次多项式.请帮忙给出正确答案和分析
设f(z)是整函数,n为正整数,试证当 时,f(z)至多是n一1次多项式.请帮忙给出正确答案和分析,谢谢!
试证试证: (1)cosh2 z—sinh2 z=1; (2)sech2 z+tanh2 z=1;
试证试证: (1)cosh2 z—sinh2 z=1; (2)sech2 z+tanh2 z=1; (3)cosh(z1+z2)=cosh z1cosh z2+sin试证: (1)cosh2 z—sinh2 z=1; (2)se
如果将下列函数按z一1的幂展开 并指明其收敛范围:将下列函数按z一1的幂展开 并指明其收敛范围: 请
如果将下列函数按z一1的幂展开,并指明其收敛范围:将下列函数按z一1的幂展开,并指明其收敛范围: 请帮忙给出正确答案和分析,谢谢!
计算:(1)∫-2-2+i (z+2) 2dz;(2) ∫0π+2i cos求积分 ∫02πa(2z
计算:(1)∫-2-2+i (z+2) 2dz;(2) ∫0π+2i cos求积分 ∫02πa(2z2+8z+1)dz 之值,其中积分路径是求积分 ∫02πa(2z2+8z+1)dz 之值,其
设|zk|=1(k=1 2 … n). 试证:请帮忙给出正确答案和分析 谢谢!
设|zk|=1(k=1,2,…,n). 试证:请帮忙给出正确答案和分析,谢谢!












