设三阶Hilbert矩阵 试用Householder变换将下列实对称矩阵约化为三对角矩阵：试用Hou
设三阶Hilbert矩阵 试用Householder变换将下列实对称矩阵约化为三对角矩阵：
试用Householder变换将下列实对称矩阵约化为三对角矩阵： 
请帮忙给出正确答案和分析，谢谢！
参考解答
481***102
2024-11-17 07:11:48
正确答案：(1)本题n＝3故只需n－2＝1次约化即可。 由式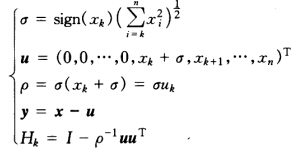
计算得 σ1＝sign(a21)
＝－5u2＝a21＋σ1＝－9 所以u＝(0－93)Tρ1＝σ1u2＝45 因此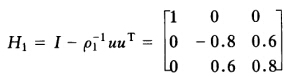
故矩阵A约化为
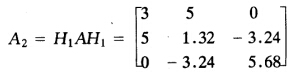(2)本题n＝4故需n－2＝＝2次约化。 当k＝＝1求H1计算A2＝H1AH1 由式计算得
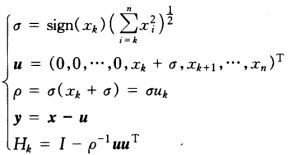σ1＝sign(a21).
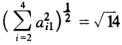＝3．741657387u2＝a2＋σ1＝6．741657387 所以u＝(06．74165738721)Tρ1＝σ1u2＝25．22497216 因此
当k＝2求H2计算A3＝H2A2H2同理计算得 σ＝sign(a32)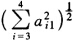
＝－2．602981028u3＝a32＋σ2＝－3．904411193所以 u＝(00－3．904411193－2．254282537)Tρ2＝σ2u3＝10．16310826 因此
所以矩阵A约化为
(1)本题n＝3,故只需n－2＝1次约化即可。由式计算得σ1＝sign(a21)＝－5,u2＝a21＋σ1＝－9所以u＝(0,－9,3)T,ρ1＝σ1u2＝45因此故矩阵A约化为(2)本题n＝4,故需n－2＝＝2次约化。当k＝＝1,求H1,计算A2＝H1AH1,由式计算得σ1＝sign(a21).＝3．741657387,u2＝a2＋σ1＝6．741657387所以u＝(0,6．741657387,2,1)T,ρ1＝σ1u2＝25．22497216因此当k＝2,求H2,计算A3＝H2A2H2,同理计算得σ＝sign(a32)＝－2．602981028,u3＝a32＋σ2＝－3．904411193所以u＝(0,0,－3．904411193,－2．254282537)T,ρ2＝σ2u3＝10．16310826因此所以矩阵A约化为
相似问题
设χ1＝37．13 χ2＝6．052 所给数字均为有效数字 试估计y＝χ1χ22的绝对误差界。请帮忙
设χ1＝37．13，χ2＝6．052，所给数字均为有效数字，试估计y＝χ1χ22的绝对误差界。请帮忙给出正确答案和分析，谢谢！
应用Euler方法解初值问题 如果用Euler法和经典Runge－Kutta方法求解初值问题 为保证
应用Euler方法解初值问题 如果用Euler法和经典Runge－Kutta方法求解初值问题 为保证数值如果用Euler法和经典Runge-Kutta方法求解初值问题 为保证数
设a＞0 为建立求设χ*是方程f(χ)＝0的一个根 f(χ)在χ*的某邻域内三次连续可微 且f(χ*
设a＞0，为建立求设χ*是方程f(χ)＝0的一个根，f(χ)在χ*的某邻域内三次连续可微，且f(χ*)≠0，对Newton法设χ*是方程f(χ)＝0的一个根，f(χ)在χ*的
用平面旋转变换和反射变换将向量x=(2 3 0 5)T变为与单位向量e1=(1 0 0 0)T平行的
用平面旋转变换和反射变换将向量x=(2，3，0，5)T变为与单位向量e1=(1，0，0，0)T平行的向量．请帮忙给出正确答案和分析，谢谢！
已知函数y＝(χ)过点(1 0) (2 －5) (3 －6) (4 3) 求经过这些点的Lagran
已知函数y＝(χ)过点(1，0)，(2，－5)，(3，－6)，(4，3)，求经过这些点的Lagrange插值多项式L3(χ)，并求f(已已知当χ＝－1，0，2，3时，对应的函数值为
