求微分方程 求解初值问题:求解初值问题: 请帮忙给出正确答案和分析 谢谢!
求微分方程 求解初值问题:
求解初值问题: 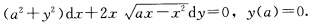
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:原方程为变量可分离方程分离变量后得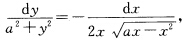 两边分别积分得到通解为
两边分别积分得到通解为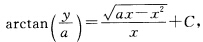 其中C为任意常数.由此得
其中C为任意常数.由此得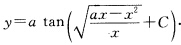 代入初值条件y(a)=0可得C=0.故所求初值问题的解为
代入初值条件y(a)=0可得C=0.故所求初值问题的解为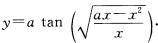
原方程为变量可分离方程,分离变量后得两边分别积分,得到通解为其中C为任意常数.由此得代入初值条件y(a)=0可得C=0.故所求初值问题的解为
相似问题
试求初值问题 设函数f(t x)在整个平面上都有定义 连续且有界 证明方程 的任一解均可延拓到整设函
试求初值问题 设函数f(t,x)在整个平面上都有定义,连续且有界,证明方程 的任一解均可延拓到整设函数f(t,x)在整个平面上都有定义,连续且有界,证明
讨论非线性方程组 构造形如V(x y)=axy2+βx3的Liapunov函数讨论下列方程组零解的稳
讨论非线性方程组 构造形如V(x,y)=axy2+βx3的Liapunov函数讨论下列方程组零解的稳定性:构造形如V(x,y)=axy2+βx3的Liapunov函数讨论下列方程组零解
试求初值问题 用逐步逼近法证明 当|λ|足够小时 积分方程 在区间[a b]上的解存在唯一.这里f(
试求初值问题 用逐步逼近法证明,当|λ|足够小时,积分方程 在区间[a,b]上的解存在唯一.这里f(t用逐步逼近法证明,当|λ|足够小时,积分方程
证明若xs(t)(s=1 2 … m)分别是方程 设复值向量函数z(t)=x(t)+iy(t)是线性
证明若xs(t)(s=1,2,…,m)分别是方程 设复值向量函数z(t)=x(t)+iy(t)是线性微分方程组 的解,其设复值向量函数z(t)=x(t)+iy(t)是线性微分方程组
验证 设A(t)是区间[α β]上的n×n阶连续矩阵函数 f(t)是区问[α β]上的不恒为零的n维
验证 设A(t)是区间[α,β]上的n×n阶连续矩阵函数,f(t)是区问[α,β]上的不恒为零的n维连续列向量.试设A(t)是区间[α,β]上的n×n阶连续矩阵函数,












