试求初值问题 用逐步逼近法证明 当|λ|足够小时 积分方程 在区间[a b]上的解存在唯一.这里f(
试求初值问题 用逐步逼近法证明,当|λ|足够小时,积分方程 在区间[a,b]上的解存在唯一.这里f(t
用逐步逼近法证明,当|λ|足够小时,积分方程 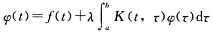 在区间[a,b]上的解存在唯一.这里f(t)为区间[a,b]上的连续函数,K(t,r)为矩形[a,b]×[a,b]上的连续函数.
在区间[a,b]上的解存在唯一.这里f(t)为区间[a,b]上的连续函数,K(t,r)为矩形[a,b]×[a,b]上的连续函数.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:构造逐步逼近迭代序列如下:
构造逐步逼近迭代序列如下:
相似问题
证明若xs(t)(s=1 2 … m)分别是方程 设复值向量函数z(t)=x(t)+iy(t)是线性
证明若xs(t)(s=1,2,…,m)分别是方程 设复值向量函数z(t)=x(t)+iy(t)是线性微分方程组 的解,其设复值向量函数z(t)=x(t)+iy(t)是线性微分方程组
验证 设A(t)是区间[α β]上的n×n阶连续矩阵函数 f(t)是区问[α β]上的不恒为零的n维
验证 设A(t)是区间[α,β]上的n×n阶连续矩阵函数,f(t)是区问[α,β]上的不恒为零的n维连续列向量.试设A(t)是区间[α,β]上的n×n阶连续矩阵函数,
(89年考研题)若齐次线性方程组位于第k个位置的数1作成多少个逆序?位于第k个位置的数1作成多少个逆
(89年考研题)若齐次线性方程组位于第k个位置的数1作成多少个逆序?位于第k个位置的数1作成多少个逆序?请帮忙给出正确答案和分析,谢谢!
证明Cauchy—Euler方程 试用矩阵指数函数思想理解并证明定理4.4.试用矩阵指数函数思想理解
证明Cauchy—Euler方程 试用矩阵指数函数思想理解并证明定理4.4.试用矩阵指数函数思想理解并证明定理4.4.请帮忙给出正确答案和分析,谢谢!
计算下述n阶行列式:请帮忙给出正确答案和分析 谢谢!
计算下述n阶行列式:请帮忙给出正确答案和分析,谢谢!












