如果设z0为解析函数f(z)的至少n阶零点 又为解析函数φ(z)的n阶零点 则(试证)设z0为解析
如果设z0为解析函数f(z)的至少n阶零点,又为解析函数φ(z)的n阶零点, 则(试证)
设z0为解析函数f(z)的至少n阶零点,又为解析函数φ(z)的n阶零点, 则(试证)
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:利用定理4.17因z0为解析函数f(z)的至少n级零点则有f(2)=(z一z0)mg(2) (m≥n)其中g(z0)=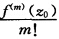 ≠0.同理 φ(z)=(z一z0)nφ(z)其中φ(z0)=
≠0.同理 φ(z)=(z一z0)nφ(z)其中φ(z0)=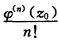 ≠0则本题得证.
≠0则本题得证.
利用定理4.17,因z0为解析函数f(z)的至少n级零点,则有f(2)=(z一z0)mg(2)(m≥n),其中g(z0)=≠0.同理φ(z)=(z一z0)nφ(z),其中φ(z0)=≠0则本题得证.
相似问题
设(1)函数f(z)在区域D内解析 f(z)≠常数; (2)C为D内任一条周线 只要设函数f(z)在
设(1)函数f(z)在区域D内解析,f(z)≠常数; (2)C为D内任一条周线,只要设函数f(z)在|z|<R内解析设函数f(z)在|z|<R内解析,令 M(r)=|f(z)| (0
判断下列复级数的敛散性 若收敛指明条件收敛还是绝对收敛. 设D是一个有界区域 其边界为aD 若fn(
判断下列复级数的敛散性,若收敛指明条件收敛还是绝对收敛. 设D是一个有界区域,其边界为aD,若fn(设D是一个有界区域,其边界为aD,若fn(z)(n=1,2,…
计算:(1)∫-2-2+i (z+2) 2dz;(2) ∫0π+2i cos设C表圆周x2+y2=3
计算:(1)∫-2-2+i (z+2) 2dz;(2) ∫0π+2i cos设C表圆周x2+y2=3,f(z)=,求f(1+i)设C表圆周x2+y2=3,f(z)=,求f(1+i)请帮忙给出正确答案和分析,谢谢!
试计算积分 ∫C(|z|—ezsin z)dz 之值 其中C为圆周|z|=a>0.请帮忙给出正确答案
试计算积分 ∫C(|z|—ezsin z)dz 之值,其中C为圆周|z|=a>0.请帮忙给出正确答案和分析,谢谢!
设连续曲线C:z=z(t) t∈[α β] 有 z(t0)≠0 (t0∈[α β) 则(试证)曲线
设连续曲线C:z=z(t),t∈[α,β],有 z(t0)≠0 (t0∈[α,β), 则(试证)曲线C在点z(t0)有切线.请帮忙给出正确答案和分析,谢谢!












