设连续曲线C：z=z(t) t∈[α β] 有 z(t0)≠0 (t0∈[α β) 则(试证)曲线
设连续曲线C：z=z(t)，t∈[α，β]，有 z(t0)≠0 (t0∈[α，β)， 则(试证)曲线C在点z(t0)有切线．
请帮忙给出正确答案和分析，谢谢！
参考解答
456***103
2024-11-21 09:42:53
正确答案：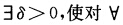
t1∈(t0一δt0+δ)＼{t0)有z(t1)≠z(t0)即C在z(t0)的对应去心邻域内无重点即能够联结割线
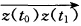否则就存在数列{tln→t0使得z(tln)=z(t0)于是有
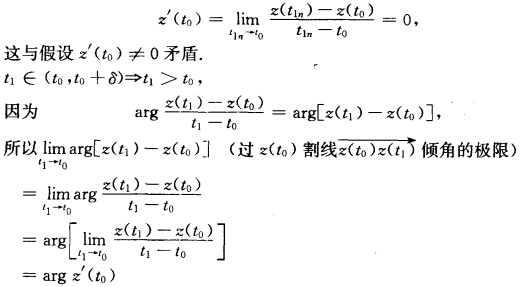因此割线确实有极限位置即曲线C在点z(t0)的切线存在其倾角为arg z'(t0)．
t1∈(t0一δ,t0+δ)＼{t0),有z(t1)≠z(t0),即C在z(t0)的对应去心邻域内无重点,即能够联结割线,否则就存在数列{tln→t0,使得z(tln)=z(t0),于是有因此,割线确实有极限位置,即曲线C在点z(t0)的切线存在,其倾角为argz'(t0)．
相似问题
若f(z) g(z)在单连通区域D内解析 α β∈D 证明∫αβ(z)g(z)dz=f(z)g(z)
若f(z)，g(z)在单连通区域D内解析，α，β∈D，证明∫αβ(z)g(z)dz=f(z)g(z)｜αβ-∫αβf(z)g(z)dz．请帮忙给出正确答案和分析，谢谢！
分别由下列条件求解析函数f(z)=u+iv． (1)u=x2+xy—y2 f(i)=一1+i； (
分别由下列条件求解析函数f(z)=u+iv． (1)u=x2+xy—y2， f(i)=一1+i； (2)u=ex(xcos y—ysin y)， f(0)=0； (3)v=， f(2)=0。请帮忙给出正确答案和分析，谢谢！
如果函数f(z)在简单闭曲线C的外部区域G内及C上每一点解析 且=a 那么(无界区域Cauchy积分
如果函数f(z)在简单闭曲线C的外部区域G内及C上每一点解析，且=a，那么(无界区域Cauchy积分公式) 请帮忙给出正确答案和分析，谢谢！
设在｜z｜≤1上函数f(z)解析 且｜f(z)｜≤1 试证： ｜f(0)｜≤1． 注：很清楚 由f
设在｜z｜≤1上函数f(z)解析，且｜f(z)｜≤1， 试证： ｜f(0)｜≤1． 注：很清楚，由f(z)=z知，这是可能的最好界．请帮忙给出正确答案和分析，谢谢！
设(1)函数f(z)在区域D内解析 f(z)≠常数； (2)C为D内任一条周线 只要函数并不是常数
设(1)函数f(z)在区域D内解析，f(z)≠常数； (2)C为D内任一条周线，只要函数并不是常数，这与唯一函数并不是常数，这与唯一性定理是否矛盾?请帮忙给出正
