设(1)函数f(z)在区域D内解析 f(z)≠常数； (2)C为D内任一条周线 只要函数并不是常数
设(1)函数f(z)在区域D内解析，f(z)≠常数； (2)C为D内任一条周线，只要函数并不是常数，这与唯一
函数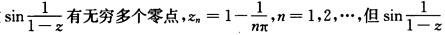
并不是常数，这与唯一性定理是否矛盾?
请帮忙给出正确答案和分析，谢谢！
参考解答
413***103
2024-11-21 09:31:51
正确答案：不矛盾．虽然
n=12…上取值为0但这个点集的唯一的一个凝聚点z0=1并不在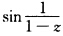
的解析域｜z｜＜1内而唯一性定理要求点集的凝聚点必须属于函数的解析域内才能由无穷点集上的值确定函数在整个解析域的值因此
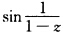不恒为零与解析函数的唯一性定理不矛盾．
不矛盾．虽然,n=1,2,…上取值为0,但这个点集的唯一的一个凝聚点z0=1,并不在的解析域｜z｜＜1内,而唯一性定理要求点集的凝聚点必须属于函数的解析域内,才能由无穷点集上的值确定函数在整个解析域的值,因此不恒为零与解析函数的唯一性定理不矛盾．
相似问题
设(1)函数f(z)在区域D内解析 f(z)≠常数； (2)C为D内任一条周线 只要求下列幂级数的收
设(1)函数f(z)在区域D内解析，f(z)≠常数； (2)C为D内任一条周线，只要求下列幂级数的收敛半径：求下列幂级数的收敛半径： 请帮忙给出正确答案和分析，谢谢！
判断下列复级数的敛散性 若收敛指明条件收敛还是绝对收敛． 将下列函数战成z的幂级数将下列函数战成z的
判断下列复级数的敛散性，若收敛指明条件收敛还是绝对收敛． 将下列函数战成z的幂级数将下列函数战成z的幂级数 请帮忙给出正确答案和分析，谢谢！
判断下列复级数的敛散性 若收敛指明条件收敛还是绝对收敛． 判断下列函数在零点z=0的阶： (1)f(
判断下列复级数的敛散性，若收敛指明条件收敛还是绝对收敛． 判断下列函数在零点z=0的阶： (1)f(z判断下列函数在零点z=0的阶： (1)f(z)=sin z—tan
计算：(1)∫－2－2＋i (z＋2) 2dz；(2) ∫0π＋2i cos(分部积分法)设函数f(
计算：(1)∫－2－2＋i (z＋2) 2dz；(2) ∫0π＋2i cos(分部积分法)设函数f(z)，g(z)在单连通区域D内解析，α、β(分部积分法)设函数f(z)，g(z)在单连
如果写出ezln(1＋z)的幂级数展式至含z5项为止 其中ln(1＋z)｜z=0=0。写出ezln(
如果写出ezln(1＋z)的幂级数展式至含z5项为止，其中ln(1＋z)｜z=0=0。写出ezln(1+z)的幂级数展式至含z5项为止，其中ln(1+z)｜z=0=0。请帮忙给出正确答案和分析，谢谢！
