设(1)函数f(z)在区域D内解析 f(z)≠常数; (2)C为D内任一条周线 只要求下列幂级数的收
设(1)函数f(z)在区域D内解析,f(z)≠常数; (2)C为D内任一条周线,只要求下列幂级数的收敛半径:
求下列幂级数的收敛半径: 
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案: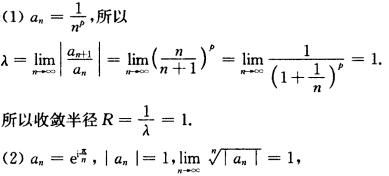 所以收敛半径R=1.
所以收敛半径R=1.
所以收敛半径R=1.
相似问题
判断下列复级数的敛散性 若收敛指明条件收敛还是绝对收敛. 将下列函数战成z的幂级数将下列函数战成z的
判断下列复级数的敛散性,若收敛指明条件收敛还是绝对收敛. 将下列函数战成z的幂级数将下列函数战成z的幂级数 请帮忙给出正确答案和分析,谢谢!
判断下列复级数的敛散性 若收敛指明条件收敛还是绝对收敛. 判断下列函数在零点z=0的阶: (1)f(
判断下列复级数的敛散性,若收敛指明条件收敛还是绝对收敛. 判断下列函数在零点z=0的阶: (1)f(z判断下列函数在零点z=0的阶: (1)f(z)=sin z—tan
计算:(1)∫-2-2+i (z+2) 2dz;(2) ∫0π+2i cos(分部积分法)设函数f(
计算:(1)∫-2-2+i (z+2) 2dz;(2) ∫0π+2i cos(分部积分法)设函数f(z),g(z)在单连通区域D内解析,α、β(分部积分法)设函数f(z),g(z)在单连
如果写出ezln(1+z)的幂级数展式至含z5项为止 其中ln(1+z)|z=0=0。写出ezln(
如果写出ezln(1+z)的幂级数展式至含z5项为止,其中ln(1+z)|z=0=0。写出ezln(1+z)的幂级数展式至含z5项为止,其中ln(1+z)|z=0=0。请帮忙给出正确答案和分析,谢谢!
试解方程: (1)ez=已知f(z)=在Ox轴上A点(OA=R>1)的初值为++1 令z由A起沿正向
试解方程: (1)ez=已知f(z)=在Ox轴上A点(OA=R>1)的初值为++1,令z由A起沿正向在以原点为中心的圆已知f(z)=在Ox轴上A点(OA=R>1)的初值为++1,令z由A












