如果函数f(z)在简单闭曲线C的外部区域G内及C上每一点解析 且=a 那么(无界区域Cauchy积分
如果函数f(z)在简单闭曲线C的外部区域G内及C上每一点解析,且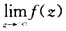 =a,那么(无界区域Cauchy积分公式)
=a,那么(无界区域Cauchy积分公式) 
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:对于任意取定的点z∈G(图3-12)取充分大的正数R0作圆周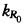 :|z|=R0包含曲线C及点z则依假设条件知f(z)在C与
:|z|=R0包含曲线C及点z则依假设条件知f(z)在C与 所围的复连通区域G'内及边界上解析根据Cauchy积分公式得
所围的复连通区域G'内及边界上解析根据Cauchy积分公式得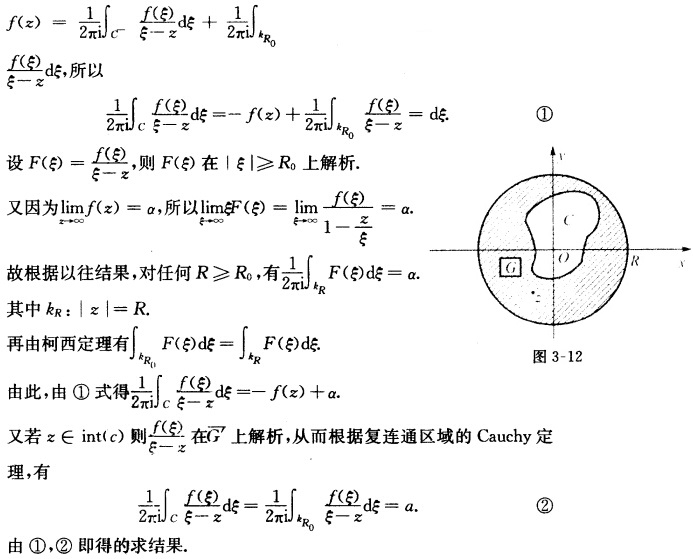
对于任意取定的点z∈G(图3-12),取充分大的正数R0,作圆周:|z|=R0,包含曲线C及点z,则依假设条件知f(z)在C与所围的复连通区域G'内及边界上解析根据Cauchy积分公式得
相似问题
设在|z|≤1上函数f(z)解析 且|f(z)|≤1 试证: |f(0)|≤1. 注:很清楚 由f
设在|z|≤1上函数f(z)解析,且|f(z)|≤1, 试证: |f(0)|≤1. 注:很清楚,由f(z)=z知,这是可能的最好界.请帮忙给出正确答案和分析,谢谢!
设(1)函数f(z)在区域D内解析 f(z)≠常数; (2)C为D内任一条周线 只要函数并不是常数
设(1)函数f(z)在区域D内解析,f(z)≠常数; (2)C为D内任一条周线,只要函数并不是常数,这与唯一函数并不是常数,这与唯一性定理是否矛盾?请帮忙给出正
设(1)函数f(z)在区域D内解析 f(z)≠常数; (2)C为D内任一条周线 只要求下列幂级数的收
设(1)函数f(z)在区域D内解析,f(z)≠常数; (2)C为D内任一条周线,只要求下列幂级数的收敛半径:求下列幂级数的收敛半径: 请帮忙给出正确答案和分析,谢谢!
判断下列复级数的敛散性 若收敛指明条件收敛还是绝对收敛. 将下列函数战成z的幂级数将下列函数战成z的
判断下列复级数的敛散性,若收敛指明条件收敛还是绝对收敛. 将下列函数战成z的幂级数将下列函数战成z的幂级数 请帮忙给出正确答案和分析,谢谢!
判断下列复级数的敛散性 若收敛指明条件收敛还是绝对收敛. 判断下列函数在零点z=0的阶: (1)f(
判断下列复级数的敛散性,若收敛指明条件收敛还是绝对收敛. 判断下列函数在零点z=0的阶: (1)f(z判断下列函数在零点z=0的阶: (1)f(z)=sin z—tan












