设A为严格对角占优矩阵 经过Gauss顺序消元法一步后 A约化为 其中a＝(a12 a13 … a1
设A为严格对角占优矩阵，经过Gauss顺序消元法一步后，A约化为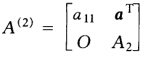
其中a＝(a12，a13，…，a1n)T，证明： (1)A2仍为严格对角占优矩阵。 (2)线性方程组Aχ＝b，由Gauss顺序消去法可求得方程组的唯一解。
请帮忙给出正确答案和分析，谢谢！
参考解答
473***102
2024-11-17 06:52:19
正确答案：(1)由假设及Gauss消元法知：对于i＝23…n有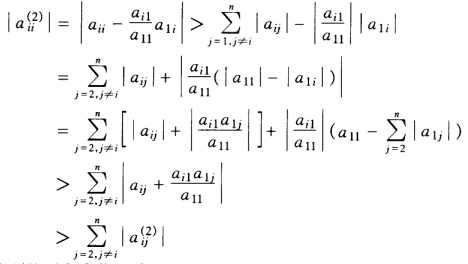
即A2仍为严格对角占优矩阵。 (2)由(1)可知Gauss顺序消去法做第k步消元时Ak为严格对角占优矩阵所以akk(k)≠0(k＝12…n)因此Gauss顺序消去法可以顺利进行求得方程组的唯一解。
(1)由假设及Gauss消元法知：对于i＝2,3,…,n,有即A2仍为严格对角占优矩阵。(2)由(1)可知,Gauss顺序消去法做第k步消元时,Ak为严格对角占优矩阵,所以akk(k)≠0(k＝1,2,…,n),因此Gauss顺序消去法可以顺利进行,求得方程组的唯一解。
相似问题
试用Aitken迭代法和Steffensen迭代法解方程χ＝e－χ的根 取χ0＝0．5。请帮忙给出正
试用Aitken迭代法和Steffensen迭代法解方程χ＝e－χ的根，取χ0＝0．5。请帮忙给出正确答案和分析，谢谢！
设P∈Rn×n为非奇异 又‖χ‖是Rn上的一种向量范数 证明： (1)是Rn上的一种向量范数； (2
设P∈Rn×n为非奇异，又‖χ‖是Rn上的一种向量范数，证明： (1)是Rn上的一种向量范数； (2)是向量范数‖χ‖*的矩阵范数。请帮忙给出正确答案和分析，谢谢！
已知函数y＝(χ)过点(1 0) (2 －5) (3 －6) (4 3) 求经过这些点的Lagran
已知函数y＝(χ)过点(1，0)，(2，－5)，(3，－6)，(4，3)，求经过这些点的Lagrange插值多项式L3(χ)，并求f(设f设f(χ)是一个n次多项式，且有n个互异的买
已知函数f(χ)＝lnχ和它的导数f′(χ)＝已知函数y＝lnx的函数表如下： 试求满足上表条件的三
已知函数f(χ)＝lnχ和它的导数f′(χ)＝已知函数y＝lnx的函数表如下： 试求满足上表条件的三次样已知函数y＝lnx的函数表如下： 试求满足上表条件的
设A B为任意非奇异矩阵 证明： (1)Cond(A)≥1； (2)Cond(AB)≤Cond(A)
设A，B为任意非奇异矩阵，证明： (1)Cond(A)≥1； (2)Cond(AB)≤Cond(A)Cond(B)。请帮忙给出正确答案和分析，谢谢！
