求微分方程 试用分离变量法求下列一阶微分方程的解.试用分离变量法求下列一阶微分方程的解. 请帮忙给出
求微分方程 试用分离变量法求下列一阶微分方程的解.
试用分离变量法求下列一阶微分方程的解. 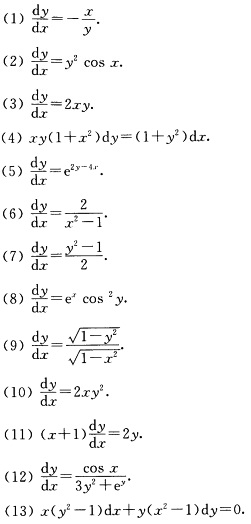
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案: 其中C1为任意常数此即
其中C1为任意常数此即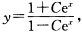 其中
其中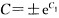 为任意非零常数.此外显然y=1和y=-1也是方程的解从而方程的解为
为任意非零常数.此外显然y=1和y=-1也是方程的解从而方程的解为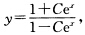 和y=-1其中C为任意常数. (8)当cosy≠0即
和y=-1其中C为任意常数. (8)当cosy≠0即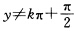 (k为整数)时分离变量后得sec2ydy=exdx两端积分得tan y=ex+C.故方程的通解为y=arctan(ex+C)其中C为任意常数.此外显然对任意的整数k
(k为整数)时分离变量后得sec2ydy=exdx两端积分得tan y=ex+C.故方程的通解为y=arctan(ex+C)其中C为任意常数.此外显然对任意的整数k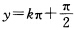 也是方程的解. (9)当Y≠±1时分离变量后得
也是方程的解. (9)当Y≠±1时分离变量后得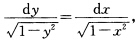 两端积分得arcsiny=arcsinx+C其中C为任意常数从而方程的通解为y=sin(arcsinx+C).此外显然y=1和y=-1也是方程的解. (10)当y≠0时分离变量后得
两端积分得arcsiny=arcsinx+C其中C为任意常数从而方程的通解为y=sin(arcsinx+C).此外显然y=1和y=-1也是方程的解. (10)当y≠0时分离变量后得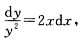 两端积分得
两端积分得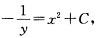 其中C为任意常数从而方程的通解为
其中C为任意常数从而方程的通解为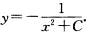 此外显然y=0也是方程的解. (11)当y≠0时分离变量后得
此外显然y=0也是方程的解. (11)当y≠0时分离变量后得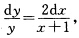 两端积分得In|y|=2In|x+1|+C1即
两端积分得In|y|=2In|x+1|+C1即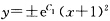 其中C1为任意常数此外显然y=0也是方程的解从而方程的通解为y=C(x+1)2其中C为任意常数. (12)分离变量后得(3y2+ey)dy=cosxdx两端积分得方程的隐式通解y3+ey=sinx+C其中C为任意常数. (13)当y≠±1时分离变量后得
其中C1为任意常数此外显然y=0也是方程的解从而方程的通解为y=C(x+1)2其中C为任意常数. (12)分离变量后得(3y2+ey)dy=cosxdx两端积分得方程的隐式通解y3+ey=sinx+C其中C为任意常数. (13)当y≠±1时分离变量后得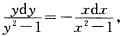 两端积分得
两端积分得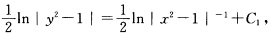 即(x2一1)(y2一1)=
即(x2一1)(y2一1)=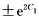 其中C1为任意常数此外显然y=±1也是方程的解从而方程的通解为(x2一1)(y2一1)=C其中C为任意常数.
其中C1为任意常数此外显然y=±1也是方程的解从而方程的通解为(x2一1)(y2一1)=C其中C为任意常数.
其中C1为任意常数,此即其中为任意非零常数.此外显然y=1和y=-1也是方程的解,从而方程的解为和y=-1,其中C为任意常数.(8)当cosy≠0,即(k为整数)时,分离变量后得sec2ydy=exdx,两端积分得tany=ex+C.故方程的通解为y=arctan(ex+C),其中C为任意常数.此外显然对任意的整数k,也是方程的解.(9)当Y≠±1时,分离变量后得两端积分得arcsiny=arcsinx+C,其中C为任意常数,从而方程的通解为y=sin(arcsinx+C).此外显然y=1和y=-1也是方程的解.(10)当y≠0时,分离变量后得两端积分得其中C为任意常数,从而方程的通解为此外显然y=0也是方程的解.(11)当y≠0时,分离变量后得两端积分得In|y|=2In|x+1|+C1,即,其中C1为任意常数,此外显然y=0也是方程的解,从而方程的通解为y=C(x+1)2,其中C为任意常数.(12)分离变量后得(3y2+ey)dy=cosxdx,两端积分得方程的隐式通解y3+ey=sinx+C,其中C为任意常数.(13)当y≠±1时,分离变量后得两端积分得即(x2一1)(y2一1)=,其中C1为任意常数,此外显然y=±1也是方程的解,从而方程的通解为(x2一1)(y2一1)=C,其中C为任意常数.
相似问题
求齐次线性方程 分析振动方程 的特征根并给出通解.这里δ≥0 ω>0.分析振动方程 的特征根并给出
求齐次线性方程 分析振动方程 的特征根并给出通解.这里δ≥0,ω>0.分析振动方程 的特征根并给出通解.这里δ≥0,ω>0.请帮忙给出正确答案和分析,谢谢!
求微分方程 求解初值问题:求解初值问题: 请帮忙给出正确答案和分析 谢谢!
求微分方程 求解初值问题:求解初值问题: 请帮忙给出正确答案和分析,谢谢!
试求初值问题 设函数f(t x)在整个平面上都有定义 连续且有界 证明方程 的任一解均可延拓到整设函
试求初值问题 设函数f(t,x)在整个平面上都有定义,连续且有界,证明方程 的任一解均可延拓到整设函数f(t,x)在整个平面上都有定义,连续且有界,证明
讨论非线性方程组 构造形如V(x y)=axy2+βx3的Liapunov函数讨论下列方程组零解的稳
讨论非线性方程组 构造形如V(x,y)=axy2+βx3的Liapunov函数讨论下列方程组零解的稳定性:构造形如V(x,y)=axy2+βx3的Liapunov函数讨论下列方程组零解
试求初值问题 用逐步逼近法证明 当|λ|足够小时 积分方程 在区间[a b]上的解存在唯一.这里f(
试求初值问题 用逐步逼近法证明,当|λ|足够小时,积分方程 在区间[a,b]上的解存在唯一.这里f(t用逐步逼近法证明,当|λ|足够小时,积分方程












