参考解答
420***103
2024-11-21 12:31:45
正确答案：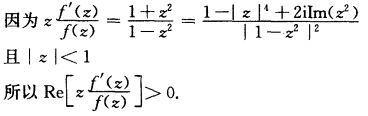
相似问题
设(1)函数f(z)在区域D内解析 f(z)≠常数； (2)C为D内任一条周线 只要为什么在区域｜z
设(1)函数f(z)在区域D内解析，f(z)≠常数； (2)C为D内任一条周线，只要为什么在区域｜z｜＜R内解析为什么在区域｜z｜＜R内解析且在区间(一R，R)取实数值
设在｜z｜＜R内解析的函数f(z)有泰勒展式 f(z)=a0+az+a22+…+azn+… 试证：
设在｜z｜＜R内解析的函数f(z)有泰勒展式 f(z)=a0+az+a22+…+azn+…， 试证：当0≤r＜R时 请帮忙给出正确答案和分析，谢谢！
若f(z)在圆｜z｜＜R内解析 f(0)=0 ｜f(z)｜≤M＜＋∞ 则 (1)｜f(z)｜≤求出下
若f(z)在圆｜z｜＜R内解析，f(0)=0，｜f(z)｜≤M＜＋∞，则 (1)｜f(z)｜≤求出下列函数的奇点，并确定它们的类别求出下列函数的奇点，并确定它们的类别(
试证：在单位圆｜z｜＜1内 级数 z+(z2一z)+…+(z2一zn-1)+…收敛于函数f(z)≡0
试证：在单位圆｜z｜＜1内，级数 z+(z2一z)+…+(z2一zn-1)+…收敛于函数f(z)≡0，但它并非一致收敛的．请帮忙给出正确答案和分析，谢谢！
判断下列复级数的敛散性 若收敛指明条件收敛还是绝对收敛． f(z)为整函数 且｜f(z)｜→f(z)
判断下列复级数的敛散性，若收敛指明条件收敛还是绝对收敛． f(z)为整函数，且｜f(z)｜→f(z)是不高于f(z)为整函数，且｜f(z)｜→f(z)是不高于n次的多项
