若f(z)在圆｜z｜＜R内解析 f(0)=0 ｜f(z)｜≤M＜＋∞ 则 (1)｜f(z)｜≤求出下

正确答案：(1)这是有理分式函数故分母的零点0一i及i是这个函数的极点下面考查它们的级． z=0是分母的一级零点又非分子z⁶+1的零点数z=0为f(z)的一级极点． 注意到z⁶+1=(z²+1)(z⁴一z²+1)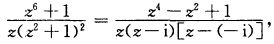可见z=±i各是分母的一级零点而不是分子的零点因此都是f(z)的一级极点． 再考查∞因为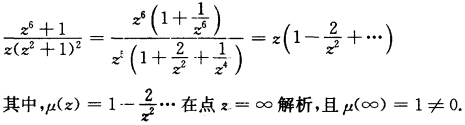由定理5．4'的(5．11)'式可见z=∞是f(z)的一级极点．(2)显然z=1是f(a)的二级极点下面考查点∞由于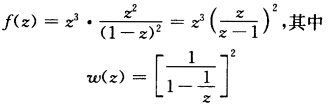在点z=∞解析且μ(∞)=1≠0可见z=∞是f(z)的三级极点．(3)f(z)只以z=0和z=∞为奇点而f(z)=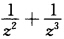就是f(z)在0＜｜z｜＜+∞内的洛朗展式．在z=0的主部为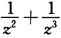故z=0为f(z)的三级极点又在z=∞的主部为零故z=∞为f(z)的可去奇点．由于f(z)=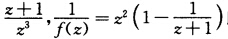以z=∞为二级极点故f(z)以z=∞为二级零点．(4)求f(z)的洛朗展式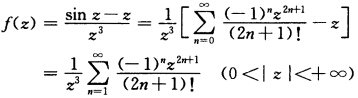由此可见f(z)在z=0的主要部分(负幂)为零；在z=∞的主要部分(正幂)有无限项故z=0为f(2)的可去奇点z=∞为f(z)的本性奇点．(5)解1+e^z=0得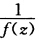的零点 z_k=(2k+1)πi (k=0±1…)又因为(1+e^z)'｜z=z_k=e^z｜z=z_k≠0故z_k都是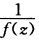的一级零点由定理5．4(3)z_k均为f(z)的一级极点．当k→∞时z_k→∞故点∞是f(z)的非孤立奇点即极点列{z_k的聚点．故cos²z以z_k=(k+)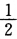π(k=0±1…)为二级零点从而sec² z就以z_k=(ki+)π(k=0±1…)为二级极点．又因当k→∞{z_k→∞故点∞为sec² z的非孤立奇点即极点列{z_k的聚点．(7)因为sin z—sina仅以kπ+(一1)^ka(k=0±1…)为孤立零点又因为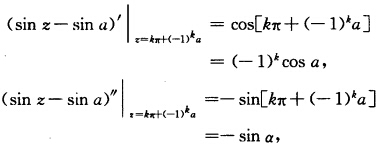所以当cosa≠0时kπ+(一1)^ka(k=0±1…)各为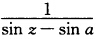的一级极点；当cosa=0时必然sina≠0因而kπ+(一1)^ka(k=0±1…)各为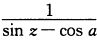的二级极点．又因极点列{kπ+(一1)^ka)→∞(k→∞)故点∞为非孤立奇点．
(1)这是有理分式函数,故分母的零点0,一i及i是这个函数的极点,下面考查它们的级．z=0是分母的一级零点,又非分子z6+1的零点,数z=0为f(z)的一级极点．注意到z6+1=(z2+1)(z4一z2+1),可见z=±i各是分母的一级零点,而不是分子的零点,因此都是f(z)的一级极点．再考查∞,因为由定理5．4'的(5．11)'式,可见z=∞是f(z)的一级极点．(2)显然z=1是f(a)的二级极点,下面考查点∞,由于在点z=∞解析,且μ(∞)=1≠0,可见z=∞是f(z)的三级极点．(3)f(z)只以z=0和z=∞为奇点,而f(z)=就是f(z)在0＜｜z｜＜+∞内的洛朗展式．在z=0的主部为,故z=0为f(z)的三级极点,又在z=∞的主部为零,故z=∞为f(z)的可去奇点．由于f(z)=以z=∞为二级极点,故f(z)以z=∞为二级零点．(4)求f(z)的洛朗展式由此可见,f(z)在z=0的主要部分(负幂)为零；在z=∞的主要部分(正幂)有无限项,故z=0为f(2)的可去奇点z=∞为f(z)的本性奇点．(5)解1+ez=0得的零点zk=(2k+1)πi(k=0,±1,…)又因为(1+ez)'｜z=zk=ez｜z=zk≠0,故zk都是的一级零点,由定理5．4(3),zk均为f(z)的一级极点．当k→∞时,zk→∞,故点∞是f(z)的非孤立奇点,即极点列{zk的聚点．故cos2z以zk=(k+)π(k=0,±1,…)为二级零点,从而sec2z就以zk=(ki+)π(k=0,±1,…)为二级极点．又因当k→∞,{zk→∞,故点∞为sec2z的非孤立奇点,即极点列{zk的聚点．(7)因为sinz—sina仅以kπ+(一1)ka(k=0,±1,…)为孤立零点,又因为所以,当cosa≠0时,kπ+(一1)ka(k=0,±1,…)各为的一级极点；当cosa=0时,必然sina≠0,因而kπ+(一1)ka(k=0,±1,…)各为的二级极点．又因极点列{kπ+(一1)ka)→∞(k→∞),故点∞为非孤立奇点．