判断下列复级数的敛散性 若收敛指明条件收敛还是绝对收敛. f(z)为整函数 且|f(z)|→f(z)
判断下列复级数的敛散性,若收敛指明条件收敛还是绝对收敛. f(z)为整函数,且|f(z)|→f(z)是不高于
f(z)为整函数,且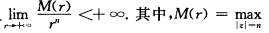 |f(z)|→f(z)是不高于n次的多项式.
|f(z)|→f(z)是不高于n次的多项式.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:因为f(z)为整函数可设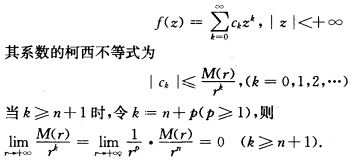 所以当k≥n+1时ck=0故f(z)是不高于n次的多项式.
所以当k≥n+1时ck=0故f(z)是不高于n次的多项式.
因为f(z)为整函数,可设所以,当k≥n+1时,ck=0,故f(z)是不高于n次的多项式.
相似问题
若函数f(z)在区域D内解析 且满足下列条件之一 试证f(z)在D内必为常数. (1)在D内f(z)
若函数f(z)在区域D内解析,且满足下列条件之一,试证f(z)在D内必为常数. (1)在D内f(z)=0; (2)在D内解析; (3)|f(z)|在D内为常数; (4)Ref(z)或Im
求积分 ∫C dz(C:|z|=1) 从而证明:∫0πecosθcos(sinθ)dθ=π。请帮忙
求积分 ∫C dz(C:|z|=1), 从而证明:∫0πecosθcos(sinθ)dθ=π。请帮忙给出正确答案和分析,谢谢!
设(1)函数f(z)在区域D内解析 f(z)≠常数; (2)C为D内任一条周线 只要将函数f(z)=
设(1)函数f(z)在区域D内解析,f(z)≠常数; (2)C为D内任一条周线,只要将函数f(z)=在z=0的邻域将函数f(z)=在z=0的邻域内展成级数。(其中0<|a|<|b|
设(1)函数f(z)在区域D内解析 f(z)≠常数; (2)C为D内任一条周线 只要全含于D; (3
设(1)函数f(z)在区域D内解析,f(z)≠常数; (2)C为D内任一条周线,只要全含于D; (3)A为任一复数.请帮忙给出正确答案和分析,谢谢!
如果指出下列函数在零点z=0的阶. (1)z2(一1); (2)6sin z3+z3(z6—6).指
如果指出下列函数在零点z=0的阶. (1)z2(一1); (2)6sin z3+z3(z6—6).指出下列函数在零点z=0的阶. (1)z2(一1); (2)6sin z3+z3(z6—6).请帮忙给出正确答案和分析,谢谢!












