用关于变量有界情形的单纯形方法解下列问题：min －x1一8x2—5x3—6x4 s．t． x1＋4

正确答案：线性规划写成下列形式： min c₁x₁+c₂x₂ s．t． A₁x₁+A₂x₂≤b x₁∈S₁ x₂∈S₂其中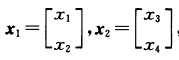c₁=[一1一8c₂=[一5一6A₁=[14A₂=[52b=7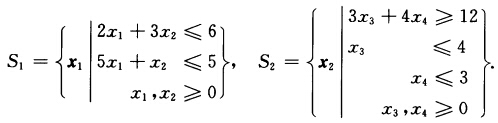．S₁和S₂均为有界集．设S₁有t₁个极点：S₂有t₂个极点：x₂⁽¹⁾¨x₂⁽²⁾…主规划写成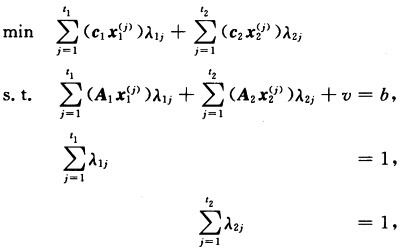 λ_1j≥0j=12…t₁λ_2j≥0j=12…t₂v≥0．下面用修正单纯形方法解主规划．先给定初始基．取S₁的一个极点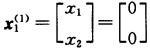S₂的一个极点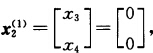初始基变量为vλ₁₁λ₂₁．构造初表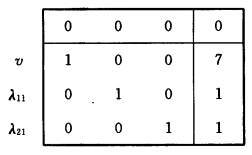： 第1次迭代： 解子规划： max (ωA₁一c₁)x₁+α₁ s．t． x₁∈S₁即 max x₁+8x₂ s．t． 2x₁+3x₂≤6 5x₁+x₂≤5 x₁x₂≥0．子规划最优解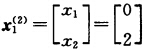最优值z₁=16．可知主规划中对应λ₁₂的判别数为16λ₁₂进基主列用表格形式计算如下： 第2次迭代： 解子规划 max(ωA₁一c₁)x₁+α₁ s．t． x₁∈S₁即 max —x₁ s．t． 2x₁+3x₂≤6 5x₁+x₂≤5 x₁x₂≥0．子规划的最优解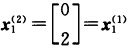最优值z₁=0．即主规划中对应λ_1j的最大判别数为0． 再解子规划 max(ωA₂一c₂)x₂+α₂ s．t． x₂∈S₂即 max 一5x₃+2x₄ s．t． 3x₃+4x₄≥12 x₃ ≤4 x₄≤3 x₃x₄≥0．用两阶段法求得子规划最优解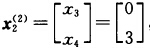．最优值z₂=6即主规划中对应λ₂₂的判别数为6λ₂₂进基主列为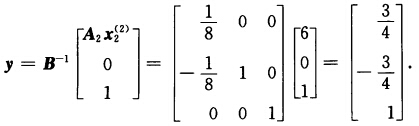用表格形式计算如下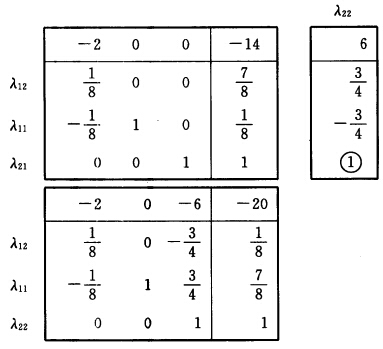： 第3次迭代： 解子规划： max(ωA₁一c₁)x₁+α₁ s．t． x₁ ∈ S₁即 max —x₁ s．t． 2x₁+3x₂≤6 5x₁+x₂≤5 x₁x₂≥0．子规划最优解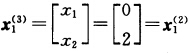最优值z₁=0． 解子规划： max(ωA₂一c₂)x₂+α₂ s．t． x₂∈S₂即 max -5x₃+2x₄—6 s．t． 3x₃+4x₄≥12 x₃ ≤4 x₄≤3x₃x₄≥0．子规划的最优解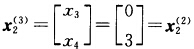最优值z₂=0．主规划已达到最优最优解是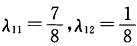：．λ₂₂=1其余变量均为非基变量取值为0． 原来问题最优解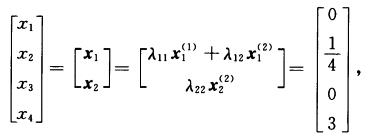：最优值f_min=一20．
线性规划写成下列形式：minc1x1+c2x2s．t．A1x1+A2x2≤bx1∈S1,x2∈S2,其中,c1=[一1,一8,c2=[一5,一6,A1=[1,4,A2=[5,2,b=7．S1和S2均为有界集．设S1有t1个极点：S2有t2个极点：x2(1)¨,x2(2),…,主规划写成λ1j≥0,j=1,2,…,t1,λ2j≥0,j=1,2,…,t2,v≥0．下面用修正单纯形方法解主规划．先给定初始基．取S1的一个极点S2的一个极点初始基变量为v,λ11,λ21．构造初表：第1次迭代：解子规划：max(ωA1一c1)x1+α1s．t．x1∈S1,即maxx1+8x2s．t．2x1+3x2≤6,5x1+x2≤5,x1,x2≥0．子规划最优解最优值z1=16．可知主规划中对应λ12的判别数为16,λ12进基,主列用表格形式计算如下：第2次迭代：解子规划max(ωA1一c1)x1+α1s．t．x1∈S1,即max—x1s．t．2x1+3x2≤6,5x1+x2≤5,x1,x2≥0．子规划的最优解最优值z1=0．即主规划中对应λ1j的最大判别数为0．再解子规划max(ωA2一c2)x2+α2s．t．x2∈S2,即max一5x3+2x4s．t．3x3+4x4≥12,x3≤4,x4≤3,x3,x4≥0．用两阶段法求得子规划最优解．最优值z2=6,即主规划中对应λ22的判别数为6,λ22进基,主列为用表格形式计算如下：第3次迭代：解子规划：max(ωA1一c1)x1+α1s．t．x1∈S1,即max—x1s．t．2x1+3x2≤6,5x1+x2≤5,x1,x2≥0．子规划最优解,最优值z1=0．解子规划：max(ωA2一c2)x2+α2s．t．x2∈S2,即max-5x3+2x4—6s．t．3x3+4x4≥12,x3≤4,x4≤3,x3,x4≥0．子规划的最优解最优值z2=0．主规划已达到最优,最优解是：．λ22=1,其余变量均为非基变量,取值为0．原来问题最优解：最优值fmin=一20．