用幂法计算矩阵设方阵A的特征值均为实数 且满足λ1>λ2≥λ3…≥λn证明取平移量p=(λ2+λn)
用幂法计算矩阵设方阵A的特征值均为实数,且满足λ1>λ2≥λ3…≥λn证明取平移量p=(λ2+λn)时,幂法收敛速
设方阵A的特征值均为实数,且满足λ1>λ2≥λ3…≥λn证明取平移量p=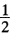 (λ2+λn)时,幂法收敛速度最快。
(λ2+λn)时,幂法收敛速度最快。
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:设平移量为P则B=A-pI的特征值为μi(λi-P)(i=12…n)。 设ei(00…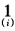 …00)T(i=12…n)则对B使用幂法有 u(k)=(λ1-p)k[α1e1+
…00)T(i=12…n)则对B使用幂法有 u(k)=(λ1-p)k[α1e1+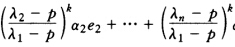 αnen 要使上式收敛速度最快即选择适当的P使
αnen 要使上式收敛速度最快即选择适当的P使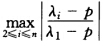 达到极小也就是使
达到极小也就是使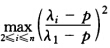 极小。 对于固定P来说(λ1-P)2是定值那么在(λ2-P)2(λ3-P)2…(λn-p)2中易知:
极小。 对于固定P来说(λ1-P)2是定值那么在(λ2-P)2(λ3-P)2…(λn-p)2中易知: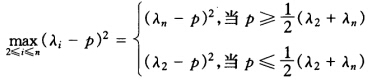 所以当p≥
所以当p≥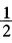 (λ1+λn)时
(λ1+λn)时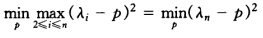 也就是在p=
也就是在p=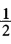 (λ2+λn)处达到极小。 当p≤
(λ2+λn)处达到极小。 当p≤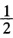 (λ2+λn)时
(λ2+λn)时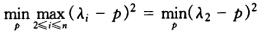 也是在p=
也是在p=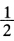 (λ2+λn)达到极小。总而言之当p=
(λ2+λn)达到极小。总而言之当p=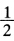 (λ2+λn)时收敛速度最快。
(λ2+λn)时收敛速度最快。
设平移量为P,则B=A-pI的特征值为μi(λi-P)(i=1,2,…,n)。设ei(0,0,…,,…,0,0)T(i=1,2,…,n),则对B使用幂法有u(k)=(λ1-p)k[α1e1+αnen要使上式收敛速度最快,即选择适当的P,使达到极小,也就是使极小。对于固定P来说,(λ1-P)2是定值,那么在(λ2-P)2,(λ3-P)2,…,(λn-p)2中,易知:所以当p≥(λ1+λn)时,也就是在p=(λ2+λn)处达到极小。当p≤(λ2+λn)时,也是在p=(λ2+λn)达到极小。总而言之,当p=(λ2+λn)时收敛速度最快。
相似问题
设定积分试确定下列求积公式中待定参数 使该求积公式的代数精度尽可能的高 并指明所构造的求积公试确定下
设定积分试确定下列求积公式中待定参数,使该求积公式的代数精度尽可能的高,并指明所构造的求积公试确定下列求积公式中待定参数,使该求积公式的代数精
设f(χ)∈Cn+1[a b] χi∈[a b](i=1 2 … n)为n个互异节点 且f(χ1)=
设f(χ)∈Cn+1[a,b],χi∈[a,b](i=1,2,…,n)为n个互异节点,且f(χ1)=1,f′(χi)=0 (i=1,2,…,n)求一不高于n次的多项式p(χ)满足:p(χ1)
用幂法计算矩阵设矩阵 试取平移量p=[2+(2-)]≈1.134 用幂法求出矩阵A的主特征值及对应的
用幂法计算矩阵设矩阵 试取平移量p=[2+(2-)]≈1.134,用幂法求出矩阵A的主特征值及对应的特征设矩阵 试取平移量p=[2+(2-)]≈1.134,用幂法求出
设A是正交矩阵 证明Cond(A)2=1。请帮忙给出正确答案和分析 谢谢!
设A是正交矩阵,证明Cond(A)2=1。请帮忙给出正确答案和分析,谢谢!
设χ∈Rn (1)‖χ‖∞≤‖χ‖1≤n‖χ‖∞; (2)‖χ‖∞≤‖χ‖2≤设A∈Rn×n 设A
设χ∈Rn, (1)‖χ‖∞≤‖χ‖1≤n‖χ‖∞; (2)‖χ‖∞≤‖χ‖2≤设A∈Rn×n,设A∈Rn×n, 请帮忙给出正确答案和分析,谢谢!












