设χ∈Rn (1)‖χ‖∞≤‖χ‖1≤n‖χ‖∞； (2)‖χ‖∞≤‖χ‖2≤设A∈Rn×n 设A
设χ∈Rn， (1)‖χ‖∞≤‖χ‖1≤n‖χ‖∞； (2)‖χ‖∞≤‖χ‖2≤设A∈Rn×n，
设A∈Rn×n，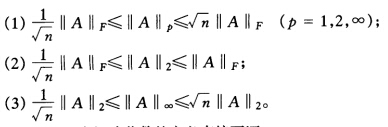 
请帮忙给出正确答案和分析，谢谢！
参考解答
4j8***102
2024-11-17 11:15:14
正确答案：×
(1)由矩阵范数的定义直接可证。(2)设ATA的特征值为λ1≥λ2≥…≥λn≥0,则有故‖A‖F≤‖A‖2≤‖A‖F成立。(3)由结论(1)和(2)可以推得：‖A‖2≤‖A‖∞。有‖χ‖∞≤‖χ‖2≤‖χ‖∞,所以对任意A∈Rn×n,χ∈Rn,则有‖Aχ‖∞≤‖Aχ‖2,‖χ‖2≤‖χ‖∞因此所以有‖A‖2≤‖A‖∞≤‖A‖2成立。
相似问题
系统误差包括_____ ________ _________ __________。系统误差的特点
系统误差包括_____、________、_________ 、__________。系统误差的特点是 ________和 _________。偶然误差的特点是__________和____________。请帮忙给出正确答案和分析，谢谢！
设函数f(χ)＝χ3＋2χ2＋7χ－5 求在等距节点χi＋1＝χi＋h(i＝0 1 … 4) h＝1
设函数f(χ)＝χ3＋2χ2＋7χ－5，求在等距节点χi＋1＝χi＋h(i＝0，1，…，4)，h＝1的前差与后差。请帮忙给出正确答案和分析，谢谢！
多次____________测定 有时出现偏差较大的数值称为__________。若测定过程中 __
多次____________测定，有时出现偏差较大的数值称为__________。若测定过程中 __________ 过失，这样的数据_________ 随意舍弃，要用___________方法
设三阶Hilbert矩阵 设矩阵将矩阵A约化为上Hessenberg矩阵。设矩阵将矩阵A约化为上He
设三阶Hilbert矩阵 设矩阵将矩阵A约化为上Hessenberg矩阵。设矩阵将矩阵A约化为上Hessenberg矩阵。请帮忙给出正确答案和分析，谢谢！
常量滴定管的读数误差为±0．01mL 滴定分析一般要求相对误差为0．1％～0．2％ 那么滴定时至少消
常量滴定管的读数误差为±0．01mL，滴定分析一般要求相对误差为0．1％～0．2％，那么滴定时至少消耗多少毫升标准溶液?这说明了什么?请帮忙给出正确答案和
