设f(χ)∈Cn+1[a b] χi∈[a b](i=1 2 … n)为n个互异节点 且f(χ1)=
设f(χ)∈Cn+1[a,b],χi∈[a,b](i=1,2,…,n)为n个互异节点,且f(χ1)=1,f′(χi)=0 (i=1,2,…,n)求一不高于n次的多项式p(χ)满足:p(χ1)=f(χ1)=1,p′(χi)=f′(χi)=0(i=1,2,…,n),并证明 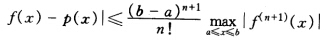
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:设p(χ)=a0+a1χ+a2χ2+…+an-1χn-1+anχn则 p′(χ)=a1+2a2χ+…+(n-1)an-1χn-2+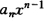 由假设p′(χi)=f′(χi)=0 i=12…n 得线性方程组 a1+2χia2+…+(n-1)χin-2+nχin-1an=0 (i=12…n) 其系数行列式为
由假设p′(χi)=f′(χi)=0 i=12…n 得线性方程组 a1+2χia2+…+(n-1)χin-2+nχin-1an=0 (i=12…n) 其系数行列式为 这里V(χ1χ2…χn)是Vandermonde行列式因为χi(i=12…n)互异所以V(χ1χ2…χn)≠0因此方程组有唯一解且 a1=a2=…=an=0 再由P(χ1)=f(χ1)得a=1故有p(χ)=1。 令R(χ)=f(χ)-p(χ)由题意 R′(χ)=f′(χ)=k(χ)ω(χ) 其中k(χ)为待定函数ω(χ)=(χ-χ1)(χ-χ2)…(χ-χn)。作辅助函数 F(χ)=f′(t)-k(χ)ω(t) 则χχ1χ2…χn是F(t)的零点反复运用Rolle定理至少存在一点ξ∈(ab)使得 F(ξ)=f(ξ)-k(χ)n!=0 所以k(χ)=
这里V(χ1χ2…χn)是Vandermonde行列式因为χi(i=12…n)互异所以V(χ1χ2…χn)≠0因此方程组有唯一解且 a1=a2=…=an=0 再由P(χ1)=f(χ1)得a=1故有p(χ)=1。 令R(χ)=f(χ)-p(χ)由题意 R′(χ)=f′(χ)=k(χ)ω(χ) 其中k(χ)为待定函数ω(χ)=(χ-χ1)(χ-χ2)…(χ-χn)。作辅助函数 F(χ)=f′(t)-k(χ)ω(t) 则χχ1χ2…χn是F(t)的零点反复运用Rolle定理至少存在一点ξ∈(ab)使得 F(ξ)=f(ξ)-k(χ)n!=0 所以k(χ)=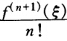 ξ∈(ab) 因此
ξ∈(ab) 因此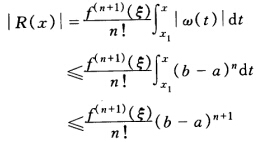 所以有|f(χ)-p(χ)|≤
所以有|f(χ)-p(χ)|≤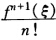 (b-a)n+1ξ∈(ab)成立。
(b-a)n+1ξ∈(ab)成立。
设p(χ)=a0+a1χ+a2χ2+…+an-1χn-1+anχn则p′(χ)=a1+2a2χ+…+(n-1)an-1χn-2+由假设p′(χi)=f′(χi)=0i=1,2,…,n得线性方程组a1+2χia2+…+(n-1)χin-2+nχin-1an=0(i=1,2,…,n)其系数行列式为这里V(χ1,χ2,…,χn)是Vandermonde行列式,因为χi(i=1,2,…,n)互异,所以V(χ1,χ2,…,χn)≠0,因此方程组有唯一解,且a1=a2=…=an=0再由P(χ1)=f(χ1)得a=1,故有p(χ)=1。令R(χ)=f(χ)-p(χ),由题意R′(χ)=f′(χ)=k(χ)ω(χ)其中k(χ)为待定函数,ω(χ)=(χ-χ1)(χ-χ2)…(χ-χn)。作辅助函数F(χ)=f′(t)-k(χ)ω(t)则χ,χ1,χ2,…,χn是F(t)的零点,反复运用Rolle定理,至少存在一点ξ∈(a,b)使得F(ξ)=f(ξ)-k(χ)n!=0所以k(χ)=,ξ∈(a,b)因此所以有|f(χ)-p(χ)|≤(b-a)n+1,ξ∈(a,b)成立。
相似问题
用幂法计算矩阵设矩阵 试取平移量p=[2+(2-)]≈1.134 用幂法求出矩阵A的主特征值及对应的
用幂法计算矩阵设矩阵 试取平移量p=[2+(2-)]≈1.134,用幂法求出矩阵A的主特征值及对应的特征设矩阵 试取平移量p=[2+(2-)]≈1.134,用幂法求出
设A是正交矩阵 证明Cond(A)2=1。请帮忙给出正确答案和分析 谢谢!
设A是正交矩阵,证明Cond(A)2=1。请帮忙给出正确答案和分析,谢谢!
设χ∈Rn (1)‖χ‖∞≤‖χ‖1≤n‖χ‖∞; (2)‖χ‖∞≤‖χ‖2≤设A∈Rn×n 设A
设χ∈Rn, (1)‖χ‖∞≤‖χ‖1≤n‖χ‖∞; (2)‖χ‖∞≤‖χ‖2≤设A∈Rn×n,设A∈Rn×n, 请帮忙给出正确答案和分析,谢谢!
系统误差包括_____ ________ _________ __________。系统误差的特点
系统误差包括_____、________、_________ 、__________。系统误差的特点是 ________和 _________。偶然误差的特点是__________和____________。请帮忙给出正确答案和分析,谢谢!
设函数f(χ)=χ3+2χ2+7χ-5 求在等距节点χi+1=χi+h(i=0 1 … 4) h=1
设函数f(χ)=χ3+2χ2+7χ-5,求在等距节点χi+1=χi+h(i=0,1,…,4),h=1的前差与后差。请帮忙给出正确答案和分析,谢谢!












