参考解答
4j8***102
2024-11-17 20:23:06
正确答案：(1)分解因式得 x(x+1)(x-1)＞0考虑方程x(x+1)(x-1)的零点0-11将数轴分为4部分分别考虑x＜-1-1＜x＜00＜x＜1x＞1。经检验-1＜x＜0或x＞1满足不等式。因此该不等式的解为 {x∈R｜-1＜x＜0或x＞1在数轴上表示如图1—1所示。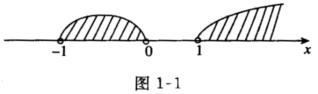
(1)分解因式得x(x+1)(x-1)＞0考虑方程x(x+1)(x-1)的零点0,-1,1,将数轴分为4部分,分别考虑x＜-1,-1＜x＜0,0＜x＜1,x＞1。经检验,-1＜x＜0或x＞1满足不等式。因此该不等式的解为{x∈R｜-1＜x＜0或x＞1在数轴上表示,如图1—1所示。
相似问题
用级数解法求埃里方程 y'-xy=0 y'-xy=u 在x=0点邻域分别满足条件y(0)=0 y(0
用级数解法求埃里方程 y "-xy=0 y "-xy=u 在x=0点邻域分别满足条件y(0)=0，y(0)=1和y(0)=1，y(0)=0的级数解。请帮忙给出正确答案和分析，谢谢！
在x=0的邻域内求解雅克比(Jacobi)方程 (1-x2)y'+[β-α-(α+β+2)x]y+λ
在x=0的邻域内求解雅克比(Jacobi)方程 (1-x2)y "+[β-α-(α+β+2)x]y+λ(α+β+λ+1)y=0， ① 其中α，β，λ均为常数。请帮忙给出正确答案和分析，谢谢！
设f(x)为可导函数 求下列各函数的一阶导数： (1)y=f(ex)ef(x)； (2)y=f(f(
设f(x)为可导函数，求下列各函数的一阶导数： (1)y=f(ex)ef(x)； (2)y=f(f(f(x)))。请帮忙给出正确答案和分析，谢谢！
设y=arcsinx。 (1)证明它满足方程(1-x2)y(n+2)-(2n+1)xy(n+1)-n
设y=arcsinx。 (1)证明它满足方程(1-x2)y(n+2)-(2n+1)xy(n+1)-n2y(n)=0(n≥0)；(2)求y(n)｜x=0。请帮忙给出正确答案和分析，谢谢！
按定义证明下列函数在其定义域内连续： (1)f(x)=1/x； (2)f(x)=｜x｜。请帮忙给出正
按定义证明下列函数在其定义域内连续： (1)f(x)=1 x； (2)f(x)=｜x｜。请帮忙给出正确答案和分析，谢谢！
