试证下列函数在z平面上解析 并分别求出其导函数． (1)f(z)=x3+3x2yi一3xy2一y3i

正确答案：(1)由u(xy)=x³一3xy²v(xy)=3x²y—y³则 u_x=3x²一3y²u_y=一6xyv_x=6xyv_y=3x²一3y² 故u_xu_yv_xv_y在z平面上连续且满足C．一R方程 u_x=v_yu_y=v_x． 所以f(z)在z平面上解析且f(z)=u+iv_x=(3x²一3y²)+i6xy=3z²． (2)因为u(xy)=e^x(xcos y—ysin y)v(xy)=e^x(ycos y+xsin y)则 u=e^x(xcos y—ysin y+cos y)u=e^x(一xsin y—ycos y—sin y) v=e^x(ycos y+xsin y+sin y)v=e^x(cos y—ysin y+xcos y) 故u_xu_yv_xv_y在z平面上连续且满足C．一R方程 u_x=v_yu_y=v_x． 所以f(z)在z平面上解析且有f'(z)=u_x+iv_x =e^x(xcos y—ysin y+cos y)+ie^x(ycos y+xsin y+sin y) =e^x[x(cos y+isin y)+iy(cos y+isin y)+(cos y+isin y) =e^x.e^iy(z+iy+1) =e^z(z+1)．(3)因为u(xy)=sin xcosh yv(xy)=cos xsinh y则u=cos xcosh yv=一sin xsinh yuy=sin xsinh yvy=cos xcosh y故u_xu_yv_xv_y在z平面上连续且满足C—R方程 u_x=v_yu_y=v_x所以f(z)在z平面上解析且f'(z)=u_x+iv_x =cos xcosh y—isin xsinh y 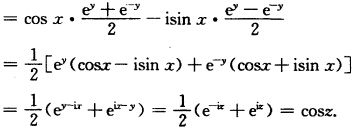(4)因为u(xy)=cos xcosh yv(xy)=一sin xsinh y则 u_x=一sin xeosh yu_y=cos x sinh y v_x=一cos x sinh yv_x=一sin xcogh y故u_xu_yv_xv_y在z平面上连续。且满足C—R方程 u_x=v_yu_y=v_x所以f(z)在z平面上解析且f'(z)=u_x+iv_x=一sin xcosh y—icos xsinh y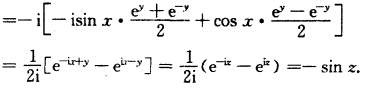
(1)由u(x,y)=x3一3xy2,v(x,y)=3x2y—y3,则ux=3x2一3y2,uy=一6xy,vx=6xy,vy=3x2一3y2,故ux,uy,vx,vy在z平面上连续,且满足C．一R方程ux=vy,uy=vx．所以f(z)在z平面上解析,且f(z)=u+ivx=(3x2一3y2)+i6xy=3z2．(2)因为u(x,y)=ex(xcosy—ysiny),v(x,y)=ex(ycosy+xsiny),则u=ex(xcosy—ysiny+cosy),u=ex(一xsiny—ycosy—siny)v=ex(ycosy+xsiny+siny),v=ex(cosy—ysiny+xcosy)故ux,uy,vx,vy在z平面上连续,且满足C．一R方程ux=vy,uy=vx．所以f(z)在z平面上解析,且有f'(z)=ux+ivx=ex(xcosy—ysiny+cosy)+iex(ycosy+xsiny+siny)=ex[x(cosy+isiny)+iy(cosy+isiny)+(cosy+isiny)=ex.eiy(z+iy+1)=ez(z+1)．(3)因为u(x,y)=sinxcoshy,v(x,y)=cosxsinhy,则u=cosxcoshy,v=一sinxsinhy,uy=sinxsinhy,vy=cosxcoshy故ux,uy,vx,vy在z平面上连续,且满足C—R方程ux=vy,uy=vx所以,f(z)在z平面上解析,且f'(z)=ux+ivx=cosxcoshy—isinxsinhy(4)因为u(x,y)=cosxcoshy,v(x,y)=一sinxsinhy,则ux=一sinxeoshy,uy=cosxsinhy,vx=一cosxsinhy,vx=一sinxcoghy故ux,uy,vx,vy在z平面上连续。且满足C—R方程ux=vy,uy=vx所以,f(z)在z平面上解析,且f'(z)=ux+ivx=一sinxcoshy—icosxsinhy