解下列线性规划问题： (1)min 5x1—6x2 S．t． x1+2x2≤10 2x1一x2≤5
解下列线性规划问题： (1)min 5x1—6x2 S．t． x1+2x2≤10， 2x1一x2≤5， x1—4x2≤4， x1，x2≥0． (2)min —x1+x2 S．t． 3x1—7x2≥8， x1一x2≤5， x1，x2≥0． (3)min 13x1+5x2 S．t． 7x1+3x2≥19， 10x1+2x2≤11， x1，x2≥0． (4)max 一20x1+10x2 S．t． x1+x2≥10， 一10x1+x2≤10， 一5x1+5x2≤25， x1+4x2≥20， x1，x2≥0． (5)min 一3x1—2x2 S．t． 3x1+2x2≤6， x1—2x2≤1， x1+x2≥1， 一x1+2x2≤1， x1，x2≥0． (6)max 5x1+4x2 S．t． 一2x1+x2≥一4， x1+2x2≤6， 5x1+3x2≤15， x1，x2≥0． (7)max 3x1+x2 s．t．x1一x2≥0， x1+x2≤5， 6x1+2x2≤21， x1，x2≥0．
请帮忙给出正确答案和分析，谢谢！
参考解答
490***101
2024-11-14 16:33:43
正确答案：(1)最优解(x1x2)=(05)最优值fmin=一30．(2)最优解(x1x2)=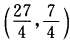
最优值fmin=一5．(3)可行域是空集不存在极小点．(4)最优解(x1x2)=
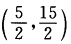最优值fmax=25．(5)最优解(x1x2)=
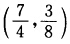最优值fmin=一6．(6)最优解(x1x2)=
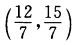最优值fmax=
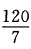(7)最优解(x1x2)=
．最优值fmax=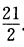
(1)最优解(x1,x2)=(0,5),最优值fmin=一30．(2)最优解(x1,x2)=,最优值fmin=一5．(3)可行域是空集,不存在极小点．(4)最优解(x1,x2)=,最优值fmax=25．(5)最优解(x1,x2)=,最优值fmin=一6．(6)最优解(x1,x2)=,最优值fmax=(7)最优解(x1,x2)=．最优值fmax=
相似问题
假设一个线性规划问题存在有限的最小值f0现在用单纯形方法求它的最优解(最小值点) 设在第k次迭代得到
假设一个线性规划问题存在有限的最小值f0现在用单纯形方法求它的最优解(最小值点)，设在第k次迭代得到一个退化的基本可行解，且只有一个基变量为零(xi=0)
给定非线性规划问题 min cTx s．t． Ax=0 xTx≤γ2 其中A为m×n矩阵(m＜n
给定非线性规划问题 min cTx s．t． Ax=0， xTx≤γ2， 其中A为m×n矩阵(m＜n)，A的秩为m，c ∈Rn且c≠0，γ是一个正数．试求问题的最优解及目标
求函数运用性质求函数的傅氏逆变换．运用性质求函数的傅氏逆变换．请帮忙给出正确答案和分析 谢谢！
求函数运用性质求函数的傅氏逆变换．运用性质求函数的傅氏逆变换．请帮忙给出正确答案和分析，谢谢！
min(4一x2)(x1—3)2 s．t． x1+x2≤3 x1 ≤2 x2≤2 x1 x2≥
min(4一x2)(x1—3)2 s．t． x1+x2≤3， x1 ≤2， x2≤2， x1，x2≥0， 取初始点x(1)=(1，2)T．请帮忙给出正确答案和分析，谢谢！
用割平面法解下列问题：min x1一2x2 s．t． x1+x2≤10 一x1+x2≤5 x1
用割平面法解下列问题：min x1一2x2 s．t． x1+x2≤10， 一x1+x2≤5， x1，x2≥0， 且为整数；请帮忙给出正确答案和分析，谢谢！
