用割平面法解下列问题：min x1一2x2 s．t． x1+x2≤10 一x1+x2≤5 x1
用割平面法解下列问题：
min x1一2x2 s．t． x1+x2≤10， 一x1+x2≤5， x1，x2≥0， 且为整数；
请帮忙给出正确答案和分析，谢谢！
参考解答
420***101
2024-11-14 16:19:40
正确答案：先用单纯形方法解松弛问题： min x1—2x2 s．t． x1+x2+x3 =10 一x1+x2 +x4=5 xj≥0 j=1234．最优表如下：
松弛问题的最优解不满足整数要求任选一个取值非整数的基变量比如取x1源约束为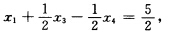
x3和x4的系数及常数项分别分解为
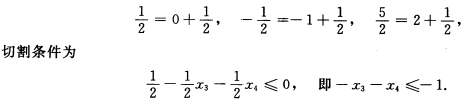将此条件置入松弛问题最优表：
用对偶单纯形方法得下表：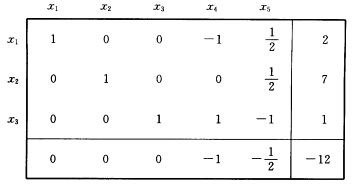
整数规划最优解(x1x2)=(27)最优值fmin=一12．
先用单纯形方法解松弛问题：minx1—2x2s．t．x1+x2+x3=10,一x1+x2+x4=5,xj≥0,j=1,2,3,4．最优表如下：松弛问题的最优解不满足整数要求,任选一个取值非整数的基变量,比如取x1,源约束为x3和x4的系数及常数项分别分解为将此条件置入松弛问题最优表：用对偶单纯形方法,得下表：整数规划最优解(x1,x2)=(2,7),最优值fmin=一12．
相似问题
考虑下列原问题 min (x1一1)2+(x2+1)2 s．t． -x1+x2一1≥0． (1)分别
考虑下列原问题 min (x1一1)2+(x2+1)2 s．t． -x1+x2一1≥0． (1)分别用图解法和最优性条件求解原问题． (2)写出对偶问题． (3)求解对偶问题． (
系统和环境既是客观存在的 又是人为划分的。此题为判断题(对 错)。请帮忙给出正确答案和分析 谢谢！
系统和环境既是客观存在的，又是人为划分的。此题为判断题(对，错)。请帮忙给出正确答案和分析，谢谢！
用起作用集方法求解下列问题：min x12－x1x2＋x22一3x1 s．t． 一x1一x2≥一2
用起作用集方法求解下列问题：min x12－x1x2＋x22一3x1 s．t． 一x1一x2≥一2， x1，x2≥0， min x12-x1x2+x22一3x1 s．t． 一x1一x2≥一2， x1
系统的状态改变时 至少有一个状态函数发生变化。此题为判断题(对 错)。请帮忙给出正确答案和分析 谢谢
系统的状态改变时，至少有一个状态函数发生变化。此题为判断题(对，错)。请帮忙给出正确答案和分析，谢谢！
定义算法映射如下： 证明A在x=2处不是闭的．请帮忙给出正确答案和分析 谢谢！
定义算法映射如下： 证明A在x=2处不是闭的．请帮忙给出正确答案和分析，谢谢！
