max 一3x1-2x2—4x3—8x4 s．t． 一2x1+5x2+3x3—5x4≤3 x1+2
max 一3x1-2x2—4x3—8x4 s．t． 一2x1+5x2+3x3—5x4≤3， x1+2x2+5x3+6x4≥8， xj≥0，j=1，2，3，4．
请帮忙给出正确答案和分析，谢谢！
参考解答
490***101
2024-11-14 17:52:30
正确答案：引进松弛变量x5x6给定初始对偶可行的基本解．问题化成 max 一3x1—2x2—4x3—8x4 s．t． 一2x1+5x2+3x3—5x4+x5=3 一x1一2x2—5x3—6x4+x6=一8 xj≥0 j=12…6． 用表格形式计算如下：
最优解(x1x2x3x4)=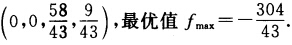
引进松弛变量x5,x6,给定初始对偶可行的基本解．问题化成max一3x1—2x2—4x3—8x4s．t．一2x1+5x2+3x3—5x4+x5=3,一x1一2x2—5x3—6x4+x6=一8,xj≥0,j=1,2,…,6．用表格形式计算如下：最优解(x1,x2,x3,x4)=
相似问题
考虑下列问题： min -x1+x2—2x3 s．t． x1+x2+x3≤6 一x1+2x2+3x
考虑下列问题： min -x1+x2—2x3 s．t． x1+x2+x3≤6， 一x1+2x2+3x3≤9， x1，x2，x3≥0． (1)用单纯形方法求出最优解． (2)假设费用系数向量c=
设S是Rn中一个非空凸集．证明对每一个整数k≥2 若x(1) x(2) … x(k)∈S 则 其中
设S是Rn中一个非空凸集．证明对每一个整数k≥2，若x(1)，x(2)，…，x(k)∈S，则 其中λ1+λ2+…+λk=1(λi≥0，i=1，2，…，k)．请帮忙给出正确答案和分析，谢谢！
min 4x1+3x2+5x3+x4+2x5 s．t． 一x1+2x2—2x3+3x4—3x5+x6
min 4x1+3x2+5x3+x4+2x5 s．t． 一x1+2x2—2x3+3x4—3x5+x6 +x8=1， x1+x2—3x3+2x4—2x5 +x8=4， 一2x3+3x4—3x5 +x7+x8=2， xj≥0，j=1，2，…，8．请帮忙给出正确答案和分析，谢谢！
min 一9x1—16x2 S．t．x1+4x2+x3 =80 2x1+3x2+x4=90 xj
min 一9x1—16x2 S．t．x1+4x2+x3 =80， 2x1+3x2+x4=90， xj≥0，j=1，2，3，4．请帮忙给出正确答案和分析，谢谢！
设A是m×n矩阵 B是l×n矩阵 c∈Rn 证明下列两个系统恰有一个有解： 系统1 Ax≤0 Bx=
设A是m×n矩阵，B是l×n矩阵，c∈Rn，证明下列两个系统恰有一个有解： 系统1 Ax≤0，Bx=0，cTx＞0，对某些x∈Rn． 系统2 ATy+BTz=c，y≥0，对某些y∈
