设A是m×n矩阵 B是l×n矩阵 c∈Rn 证明下列两个系统恰有一个有解：系统1 Ax≤0 Bx=

大学本科已帮助：人时间:2024-11-14 17:24:06

设A是m×n矩阵，B是l×n矩阵，c∈Rn，证明下列两个系统恰有一个有解：系统1 Ax≤0，Bx=0，cTx＞0，对某些x∈Rn．系统2 ATy+BTz=c，y≥0，对某些y∈Rm和z ∈Rl．
请帮忙给出正确答案和分析，谢谢！

463***101

2024-11-14 17:24:06



正确答案：由于Bx=0等价于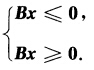因此系统1有解即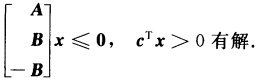根据Farkas定理得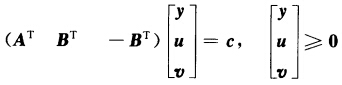无解．记u一v=z即得 A^Ty+B^Tz=c y≥0无解．反之亦然．
由于Bx=0等价于因此系统1有解,即根据Farkas定理,得无解．记u一v=z,即得ATy+BTz=c,y≥0无解．反之亦然．

指出下列函数在零点z=0的级：计算下列积分(利用留数圆周均取正向)．计算下列积分(利用留数圆周

指出下列函数在零点z=0的级：计算下列积分(利用留数，圆周均取正向)．计算下列积分(利用留数，圆周均取正向)．请帮忙给出正确答案和分析，谢谢！
设有3个产地4个销地的运输问题产量ai 销量bi及单位运价cij的数值如下表： (1)转化成产销

设有3个产地4个销地的运输问题，产量ai，销量bi及单位运价cij的数值如下表： (1)转化成产销平衡运输问题； (2)用西北角法求一基本可行解，并由此出发
证明方程z7－z3+12=0的根都在圆环域1≤|z|≤2内．请帮忙给出正确答案和分析谢谢！

证明方程z7－z3+12=0的根都在圆环域1≤|z|≤2内．请帮忙给出正确答案和分析，谢谢！
求下列幂级数的收敛半径将函数在z=0处展开为幂级数．将函数在z=0处展开为幂级数．请帮忙给出正确答

求下列幂级数的收敛半径将函数在z=0处展开为幂级数．将函数在z=0处展开为幂级数．请帮忙给出正确答案和分析，谢谢！
指出下列函数在零点z=0的级：求下列函数f(z)在扩充复平面上的奇点并判别类型．求下列函数f(z

指出下列函数在零点z=0的级：求下列函数f(z)在扩充复平面上的奇点，并判别类型．求下列函数f(z)在扩充复平面上的奇点，并判别类型．请帮忙给出正确答

指出下列函数在零点z=0的级：计算下列积分(利用留数圆周均取正向)．计算下列积分(利用留数圆周