min —x1一x2 s．t． 1一x12一x22=0；请帮忙给出正确答案和分析 谢谢！
min —x1一x2 s．t． 1一x12一x22=0；
请帮忙给出正确答案和分析，谢谢！
参考解答
481***101
2024-11-14 12:10:40
正确答案：记f(x)=一x1一x2h(x)=1一x12一x22．定义罚函数 F(xσ)=f(x)+σh2(x)=一x1一x2+σ(1一x12—x22)2 σ＞0很大．令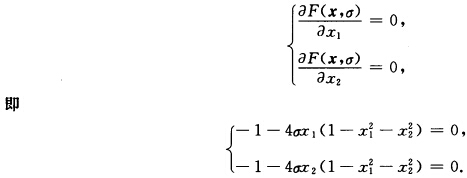
当点x不在可行域上时1一x12一x22≠0由上式得x1=x2代入上式则有 8σx13一4σx1—1=0即
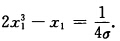由于有界闭域上的连续函数存在极小点可令σ→+∞则
记f(x)=一x1一x2,h(x)=1一x12一x22．定义罚函数F(x,σ)=f(x)+σh2(x)=一x1一x2+σ(1一x12—x22)2,σ＞0,很大．令当点x不在可行域上时,1一x12一x22≠0,由上式得x1=x2,代入上式,则有8σx13一4σx1—1=0,即由于有界闭域上的连续函数存在极小点,可令σ→+∞,则
相似问题
考虑下列问题： 设p(1) p(2) … p(n)∈Rn为一组线性无关向量 H是n阶对称正定矩阵 令
考虑下列问题： 设p(1)，p(2)，…，p(n)∈Rn为一组线性无关向量，H是n阶对称正定矩阵，令向量d(k)为 设p(1)，p(2)，…，p(n)∈Rn为一组线性无关向量，H
假设有一个路网如下图所示 图中数字表示该路段的长度 求从A到E的最短路线及其长度． max x12
假设有一个路网如下图所示，图中数字表示该路段的长度，求从A到E的最短路线及其长度． max x12＋max x12+8x2+3x32 s．t． x1+x2+2x3≤6， x1，x2，
用Zoutendijk方法求解下列问题： min x12+4x22一34x1一32x2 s．t． 2
用Zoutendijk方法求解下列问题： min x12+4x22一34x1一32x2 s．t． 2x1+x2≤6， x2≤2， x1，x2≥0， 取初始点x(1)=(1，2)T．请帮忙给出正确答案和分析，谢谢！
给定函数 f(x)=100(x2一x12)2＋(1一x1)2． 求在以下各点处的最速下降方向： 设有
给定函数 f(x)=100(x2一x12)2＋(1一x1)2． 求在以下各点处的最速下降方向： 设有函数 其设有函数 其中A为对称正定矩阵．又设x(1)(≠x)可表示为
在写热化学方程式时 用符号____________表示气态 用符号____________表示液态
在写热化学方程式时，用符号____________表示气态，用符号____________表示液态，用符号_______________表示固态。请帮忙给出正确答案和分析，谢谢！
