假设有一个路网如下图所示 图中数字表示该路段的长度 求从A到E的最短路线及其长度． max x12

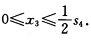正确答案：先用逆推解法．划分为3个阶段阶段指标v₃(x₃)=3x₃²v₂(x₂)=8x₂v₁(x₁)=x₁²．状态转移方程： s₃—2x₃=0s₃=s₂一x₂s₂=s₁一x₁s₁≤6? 基本方程： 由于求最大值令s₁=6．利用状态转移方程由s₁=6x₁=0推得s₂=6故x₂=6s₃=0x₃=0．最优解x=(060)最优值f_max=48．再用顺推解法．划分为3个阶段．阶段指标v₁(x₁)=x₁²v₂(x₂)=8x₂v₃(x₃)=3x₃²．状态转移方程： s₁=s₂一x₁=0s₂=s₃一x₂s₃=s₄—2x₃s₄≤6．由于变量有非负的限制因此x₁=s₂0≤x₂≤s₃基本方程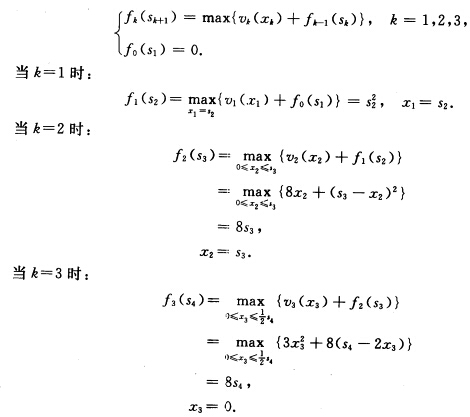： 为取最大值令s₄=6x₃=0．利用状态转移方程推出s₃=s₄一2x₃=6x₂=6s₂=s₃一x₂=0x₁=s₂=0． 最优解x=(060)最优值f_max=48．
先用逆推解法．划分为3个阶段,阶段指标v3(x3)=3x32,v2(x2)=8x2,v1(x1)=x12．状态转移方程：s3—2x3=0,s3=s2一x2,s2=s1一x1,s1≤6?基本方程：由于求最大值,令s1=6．利用状态转移方程,由s1=6,x1=0推得s2=6,故x2=6,s3=0,x3=0．最优解x=(0,6,0),最优值fmax=48．再用顺推解法．划分为3个阶段．阶段指标v1(x1)=x12,v2(x2)=8x2,v3(x3)=3x32．状态转移方程：s1=s2一x1=0,s2=s3一x2,s3=s4—2x3,s4≤6．由于变量有非负的限制,因此x1=s2,0≤x2≤s3,基本方程：为取最大值,令s4=6,x3=0．利用状态转移方程,推出s3=s4一2x3=6,x2=6,s2=s3一x2=0,x1=s2=0．最优解x=(0,6,0),最优值fmax=48．