用Zoutendijk方法求解下列问题： min x12+4x22一34x1一32x2 s．t． 2

正确答案：将问题写作： min x₁²+4x₂²一34x₁—32x₂ s．t． 一2x₁一x₂≥一6 一x₂≥一2 x₁x₂≥0目标函数的梯度▽f(x)=第1次迭代：在点起作用约束和不起作用约束的系数矩阵分别记为min ▽f(x⁽¹⁾)^Tds．t． A₁d≥0 |d₁|≤1|d₂|≤1．用单纯形方法求得 再从x⁽¹⁾出发沿可行下降方向d⁽¹⁾搜索： min f(x⁽¹⁾+λd⁽¹⁾) s．t．0≤λ≤λ_max (1)其中λ_max是步长λ的上限．为使后继点是可行点λ必须满足 A₂(x⁽¹⁾+λd⁽¹⁾)≥b₂．记问题(1)即 min (1+λ)²一34λ—82 s．t．0≤λ≤1．解得λ₁=1后继点第2次迭代：在x⁽²⁾处起作用约束和不起作用约束系数矩阵分别记为相应的约束右端记为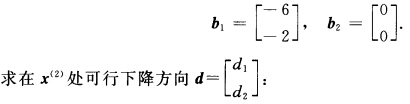min ▽f(x⁽²⁾)^Tds．t． A₁d≥0 |d₁|≤1 |d₂|≤1．用单纯形方法求得d⁽²⁾=(00)^T．根据教材中定理12．1．2x⁽²⁾=(22)^T是K—T点．由于给定问题是凸规划因此x⁽²⁾也是最优解最优值f_min=一112．
将问题写作：minx12+4x22一34x1—32x2s．t．一2x1一x2≥一6一x2≥一2x1,x2≥0目标函数的梯度▽f(x)=第1次迭代：在点,起作用约束和不起作用约束的系数矩阵分别记为min▽f(x(1))Tds．t．A1d≥0,|d1|≤1,|d2|≤1．用单纯形方法,求得再从x(1)出发,沿可行下降方向d(1)搜索：minf(x(1)+λd(1))s．t．0≤λ≤λmax(1)其中λmax是步长λ的上限．为使后继点是可行点,λ必须满足A2(x(1)+λd(1))≥b2．记问题(1)即min(1+λ)2一34λ—82s．t．0≤λ≤1．解得λ1=1,后继点第2次迭代：在x(2)处起作用约束和不起作用约束系数矩阵分别记为相应的约束右端记为min▽f(x(2))Tds．t．A1d≥0,|d1|≤1,|d2|≤1．用单纯形方法求得d(2)=(0,0)T．根据教材中定理12．1．2,x(2)=(2,2)T是K—T点．由于给定问题是凸规划,因此x(2)也是最优解,最优值fmin=一112．