考虑下列问题: min —x1—3x2 s.t. x1+x2≤6 一x1+2x2≤6 x1 x2
考虑下列问题: min —x1—3x2 s.t. x1+x2≤6, 一x1+2x2≤6, x1,x2≥0. (1)用单纯形方法求出最优解. (2)将约束右端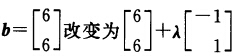 ,λ≥0,求含参数线性规划的最优解.
,λ≥0,求含参数线性规划的最优解.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)将所求问题化为标准形式用单纯形方法求解: min —x1一3x2 s.t. x1+x2+x3 =6 一x1+2x2 +x4=6xj≥0 j=1234.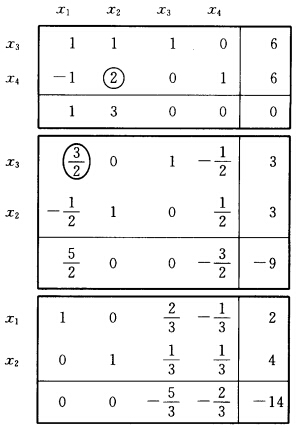 最优解(x1x2x3x4)=(2400)最优值fmin=一14. (2)将含参数线性规划化为标准形式: min —x1—3x2 s.t. x1+x2+x3 =6一λ 一x1+2x2 +x4=6+λ xj≥0 j=1234. 修改问题(1)中的最优表:
最优解(x1x2x3x4)=(2400)最优值fmin=一14. (2)将含参数线性规划化为标准形式: min —x1—3x2 s.t. x1+x2+x3 =6一λ 一x1+2x2 +x4=6+λ xj≥0 j=1234. 修改问题(1)中的最优表: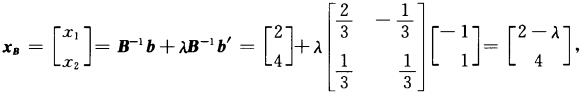 f(λ)=cBxB=一14+λ.在现行基下参数规划的单纯形表如下:
f(λ)=cBxB=一14+λ.在现行基下参数规划的单纯形表如下: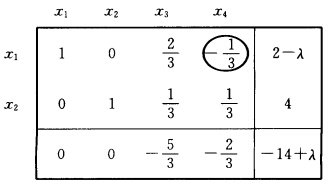 当λ∈[02时最优解(x1x2x3x4)=(2-λ400)最优值f*(λ)=-14+λ.当λ>2时2一λ<0用对偶单纯形法得下表:
当λ∈[02时最优解(x1x2x3x4)=(2-λ400)最优值f*(λ)=-14+λ.当λ>2时2一λ<0用对偶单纯形法得下表: 当λ∈[26时最优解(x1x2x3x4)=(06-λ0一6+3λ)最优值f*(λ)=一18+3λ. 当λ>6时无可行解.
当λ∈[26时最优解(x1x2x3x4)=(06-λ0一6+3λ)最优值f*(λ)=一18+3λ. 当λ>6时无可行解.
(1)将所求问题化为标准形式,用单纯形方法求解:min—x1一3x2s.t.x1+x2+x3=6,一x1+2x2+x4=6,xj≥0,j=1,2,3,4.最优解(x1,x2,x3,x4)=(2,4,0,0),最优值fmin=一14.(2)将含参数线性规划化为标准形式:min—x1—3x2s.t.x1+x2+x3=6一λ,一x1+2x2+x4=6+λ,xj≥0,j=1,2,3,4.修改问题(1)中的最优表:f(λ)=cBxB=一14+λ.在现行基下,参数规划的单纯形表如下:当λ∈[0,2时,最优解(x1,x2,x3,x4)=(2-λ,4,0,0),最优值f*(λ)=-14+λ.当λ>2时,2一λ<0,用对偶单纯形法,得下表:当λ∈[2,6时,最优解(x1,x2,x3,x4)=(0,6-λ,0,一6+3λ),最优值f*(λ)=一18+3λ.当λ>6时,无可行解.
相似问题
解下列线性规划问题: (1)min 5x1—6x2 S.t. x1+2x2≤10 2x1一x2≤5
解下列线性规划问题: (1)min 5x1—6x2 S.t. x1+2x2≤10, 2x1一x2≤5, x1—4x2≤4, x1,x2≥0. (2)min —x1+x2 S.t. 3x1—7x2≥8,
假设一个线性规划问题存在有限的最小值f0现在用单纯形方法求它的最优解(最小值点) 设在第k次迭代得到
假设一个线性规划问题存在有限的最小值f0现在用单纯形方法求它的最优解(最小值点),设在第k次迭代得到一个退化的基本可行解,且只有一个基变量为零(xi=0)
给定非线性规划问题 min cTx s.t. Ax=0 xTx≤γ2 其中A为m×n矩阵(m<n
给定非线性规划问题 min cTx s.t. Ax=0, xTx≤γ2, 其中A为m×n矩阵(m<n),A的秩为m,c ∈Rn且c≠0,γ是一个正数.试求问题的最优解及目标
求函数运用性质求函数的傅氏逆变换.运用性质求函数的傅氏逆变换.请帮忙给出正确答案和分析 谢谢!
求函数运用性质求函数的傅氏逆变换.运用性质求函数的傅氏逆变换.请帮忙给出正确答案和分析,谢谢!
min(4一x2)(x1—3)2 s.t. x1+x2≤3 x1 ≤2 x2≤2 x1 x2≥
min(4一x2)(x1—3)2 s.t. x1+x2≤3, x1 ≤2, x2≤2, x1,x2≥0, 取初始点x(1)=(1,2)T.请帮忙给出正确答案和分析,谢谢!












