已知α1 α2 α3 α4是R4的一个最大无关组 且 求证：β1 β2 β3 β4也是R4的一个最
已知α1，α2，α3，α4是R4的一个最大无关组，且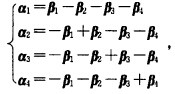 
求证：β1，β2，β3，β4也是R4的一个最大无关组。
请帮忙给出正确答案和分析，谢谢！
参考解答
473***101
2024-11-13 00:39:37
正确答案：由于向量组α1α2α3α4可由向量组β1β2β3β4线性表示且向量组α1α2α3α4线性无关因此R(β1β2β3β4)≥R(α1α2α3α4)=4又显然R(β1β2β3β4)≤4因此R(β1β2β3β4)4故β1β2β3β4线性无关又R4的最大无关组含4个向量故β1β2β3β4也是R4的一个最大无关组。
只需证明β1，β2，β3，β4线性无关。
相似问题
设矩阵A=|A3＋E|。|A3+E|。请帮忙给出正确答案和分析 谢谢！
设矩阵A=|A3＋E|。|A3+E|。请帮忙给出正确答案和分析，谢谢！
检验下列集合是否构成R3的子空间。 请帮忙给出正确答案和分析 谢谢！
检验下列集合是否构成R3的子空间。 请帮忙给出正确答案和分析，谢谢！
已知向量组 若向量组α β y线性无关 问向量组α＋β β＋γ γ＋α是否也线性无关?若向量组α β
已知向量组 若向量组α，β，y线性无关，问向量组α＋β，β＋γ，γ＋α是否也线性无关?若向量组α，β，y线性无关，问向量组α＋β，β＋γ，γ＋α是
设在贝努利试验中 事件A出现的概率为P 0＜p＜1．将贝努利试验重复独立地一直做下去 称为可列贝努利
设在贝努利试验中，事件A出现的概率为P，0＜p＜1．将贝努利试验重复独立地一直做下去，称为可列贝努利试验．证明在可列贝努利试验中，“事件A终将出现”
求矩阵A=求下列矩阵的特征值及特征向量。求下列矩阵的特征值及特征向量。 请帮忙给出正确答案和分析 谢
求矩阵A=求下列矩阵的特征值及特征向量。求下列矩阵的特征值及特征向量。 请帮忙给出正确答案和分析，谢谢！
