试证：证明：只有一个不动点(二重有限)p的分式线性变换可写成 ＋k k是非零复常数．证明：只有一个不
试证：证明：只有一个不动点(二重有限)p的分式线性变换可写成 ＋k，k是非零复常数．
证明：只有一个不动点(二重有限)p的分式线性变换可写成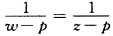 
+k，k是非零复常数．
请帮忙给出正确答案和分析，谢谢！
参考解答
463***103
2024-11-21 07:32:22
正确答案：设所求线性变换为 w=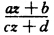
(ad一bc≠0) ① 其不动点z满足方程 cz2一(a—d)z—b=0(c≠0) ② ②的二根设为pq则 cp2一(a一d)p—b=0 cq2一(a一d)q—b=0 由①得 b一dp=一p(a—cp) ①' 由②得 b一dp=一q(a--cq) ②'
设所求线性变换为w=(ad一bc≠0)①其不动点z满足方程cz2一(a—d)z—b=0(c≠0)②②的二根设为p,q,则cp2一(a一d)p—b=0cq2一(a一d)q—b=0由①得b一dp=一p(a—cp)①'由②得b一dp=一q(a--cq)②'
相似问题
设幂级数f(z)=所表示的和函数f(z)在其收敛圆周上只有唯一的一阶极点z0．试证：→｜z0｜(｜z
设幂级数f(z)=所表示的和函数f(z)在其收敛圆周上只有唯一的一阶极点z0．试证：→｜z0｜(｜z0｜=r是收敛半径)．请帮忙给出正确答案和分析，谢谢！
若事件A与B同时发生时 事件C必发生 则下列结沦正确的是( )．A．P(C)=P(AB)B．P(C)
若事件A与B同时发生时，事件C必发生，则下列结沦正确的是( )．A．P(C)=P(AB)B．P(C)=P(A U B)C．PC≥P(A)+P(B)一lD．P(C)≤P(A)+P(B一1)请帮忙给出正确答案和分析，谢谢！
将扩充z平面割去1+i到2+2i的线段后剩下的区域共形映射成上半平面．请帮忙给出正确答案和分析 谢谢
将扩充z平面割去1+i到2+2i的线段后剩下的区域共形映射成上半平面．请帮忙给出正确答案和分析，谢谢！
证明：函数z-2是函数 由区域｜z+1｜＜1向外的解析延拓．请帮忙给出正确答案和分析 谢谢！
证明：函数z-2是函数 由区域｜z+1｜＜1向外的解析延拓．请帮忙给出正确答案和分析，谢谢！
刘维尔定理的几何意义是“非常数整函数的值不能全含于一圆之内” 试证明：非常数整函数的值不能全含于一圆
刘维尔定理的几何意义是“非常数整函数的值不能全含于一圆之内”，试证明：非常数整函数的值不能全含于一圆之外．请帮忙给出正确答案和分析，谢谢！
