设函数f(z)不恒为常数 且在0＜｜z一a｜＜R内解析 如果a是f(z)的零点的极限点 试证a必为f

正确答案：首先证明a为f(z)的奇点我们用反证法．设a不是f(z)的奇点而a又为f(z)零点的极限点则a为f(z)的非孤立零点必存在一个圆域｜z一a｜＜ρ＜R使f(z)≡0．由唯一性定理在｜z一a｜＜R内f(z)≡0与题设矛盾故a为f(z)的孤立奇点．其次证明a为f(z)的本性奇点．因为f(z)在0＜｜z一a｜＜R内解析且以a为孤立奇点故f(z)在0＜｜z—a｜＜R内可展开成级数f(z)=…+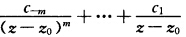+c₀+c₁(z一z₀)+c₂(z一z₀)²+……显然①上式不可能无负幂项否则z=a为可去奇点或解析点即f(z)≡常数这与题设矛盾．②上式不可能有有限个负幂项否则z=a为f(z)的极点=∞即对任意一个M＞0当0＜｜z一a｜＜r＜R时｜f(z)｜＞M这与a为f(z)零点的极限点矛盾故z=a为本性奇点．
首先证明a为f(z)的奇点,我们用反证法．设a不是f(z)的奇点,而a又为f(z)零点的极限点,则a为f(z)的非孤立零点,必存在一个圆域｜z一a｜＜ρ＜R,使f(z)≡0．由唯一性定理,在｜z一a｜＜R内,f(z)≡0与题设矛盾,故a为f(z)的孤立奇点．其次证明a为f(z)的本性奇点．因为f(z)在0＜｜z一a｜＜R内解析,且以a为孤立奇点,故f(z)在0＜｜z—a｜＜R内可展开成级数f(z)=…++c0+c1(z一z0)+c2(z一z0)2+……显然,①上式不可能无负幂项,否则z=a为可去奇点或解析点,即f(z)≡常数,这与题设矛盾．②上式不可能有有限个负幂项,否则z=a为f(z)的极点,=∞,即对任意一个M＞0,当0＜｜z一a｜＜r＜R时,｜f(z)｜＞M,这与a为f(z)零点的极限点矛盾,故z=a为本性奇点．