设χ∈Rn (1)‖χ‖∞≤‖χ‖1≤n‖χ‖∞； (2)‖χ‖∞≤‖χ‖2≤设线性方程组Aχ＝b
设χ∈Rn， (1)‖χ‖∞≤‖χ‖1≤n‖χ‖∞； (2)‖χ‖∞≤‖χ‖2≤设线性方程组Aχ＝b的系数矩阵为 (1)
设线性方程组Aχ＝b的系数矩阵为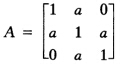 
(1)当a取值在什么范围，Jacobi迭代法收敛? (2)当a取值在什么范围，Gauss-Seidel迭代法收敛?
请帮忙给出正确答案和分析，谢谢！
参考解答
463***102
2024-11-17 07:42:57
正确答案：(1)由于Jacobi迭代矩阵为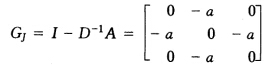
由｜λI－GJ｜＝λ3－2a2λ＝0解得λ＝0
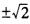a所以ρ(GJ)＝
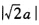。 因为Jacobi迭代法收敛条件为ρ(GJ)＜1所以
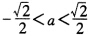。 (2)由于Gauss—Seidel迭代矩阵为
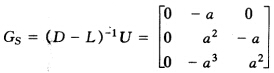由｜λI－GS｜＝λ(λ－a2)2－a4λ＝0解得λ＝02a2所以ρ(GS)＝｜2a2｜。 因为G-S迭代法收敛条件为ρ(GS)＝2a2＜1所以
。
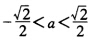(1)由于Jacobi迭代矩阵为由｜λI－GJ｜＝λ3－2a2λ＝0,解得λ＝0,a,所以ρ(GJ)＝。因为Jacobi迭代法收敛条件为ρ(GJ)＜1,所以。(2)由于Gauss—Seidel迭代矩阵为由｜λI－GS｜＝λ(λ－a2)2－a4λ＝0,解得λ＝0,2a2所以ρ(GS)＝｜2a2｜。因为G-S迭代法收敛条件为ρ(GS)＝2a2＜1,所以。
相似问题
已知KcNH．一1．79×10～ 计算0．50mol／L NH4 N03溶液的Ph＝________
已知KcNH．一1．79×10～，计算0．50mol／L NH4 N03溶液的Ph＝___________。请帮忙给出正确答案和分析，谢谢！
已知函数y＝(χ)过点(1 0) (2 －5) (3 －6) (4 3) 求经过这些点的Lagran
已知函数y＝(χ)过点(1，0)，(2，－5)，(3，－6)，(4，3)，求经过这些点的Lagrange插值多项式L3(χ)，并求f(单单调连续函数y＝f(χ)的函数值见表4．2．2
设矩阵A＝M－N 其中M为非奇异矩阵 将线性方程组Aχ＝b改写成迭代格式：χ＝Gχ＋f (k＝0 1
设矩阵A＝M－N，其中M为非奇异矩阵，将线性方程组Aχ＝b改写成迭代格式：χ＝Gχ＋f (k＝0，1，2，…)其中G＝M-1N，f＝M-1b，若‖N‖＜，证明：ρ(G)＜1
设f(χ)∈C2[a b] L1(χ)是f(χ)在[a b]上的线性插值函数 证明： 并举一例 指
设f(χ)∈C2[a，b]，L1(χ)是f(χ)在[a，b]上的线性插值函数，证明： 并举一例，指出上述不等式等号可以成立。又若f(a)＝f(b)＝0，则有何结论?请帮忙
设f(χ)＝sinχ的函数表如下： 已知函数y＝f(χ)的函数表如下： 试分别用待定系数法和带重节点
设f(χ)＝sinχ的函数表如下： 已知函数y＝f(χ)的函数表如下： 试分别用待定系数法和带重节点已知函数y＝f(χ)的函数表如下： 试分别用待定系数法
