设f(χ)＝sinχ的函数表如下： 已知函数y＝f(χ)的函数表如下： 试分别用待定系数法和带重节点
设f(χ)＝sinχ的函数表如下： 已知函数y＝f(χ)的函数表如下： 试分别用待定系数法和带重节点
已知函数y＝f(χ)的函数表如下：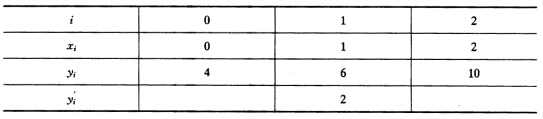 
试分别用待定系数法和带重节点差商的Newton插值法求一不超过三次的插值多项式P(χ)，且满足P(χi)＝yi(i＝0，1，2)，P′(χ1)＝y′1。
请帮忙给出正确答案和分析，谢谢！
参考解答
420***102
2024-11-17 07:24:32
正确答案：设P(χ)＝aχ3＋bχ2＋cχ＋d由题设条件有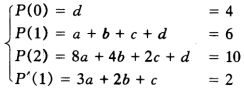
解得a＝1b＝2C＝3d＝4即P(χ)＝χ3－2χ2＋3χ＋4。 由带重节点的差商构造差商表如下：
所以N3(χ)＝4＋2χ＋χ(χ－1)2即N3(χ)=χ3－2χ2＋3χ＋4
设P(χ)＝aχ3＋bχ2＋cχ＋d,由题设条件有解得a＝1,b＝2,C＝3,d＝4,即P(χ)＝χ3－2χ2＋3χ＋4。由带重节点的差商构造差商表如下：所以N3(χ)＝4＋2χ＋χ(χ－1)2,即N3(χ)=χ3－2χ2＋3χ＋4
相似问题
设函数f(χ)＝ 根据在节点χ＝100 101 102 103 104 105处的函数值 用五点法求
设函数f(χ)＝，根据在节点χ＝100，101，102，103，104，105处的函数值，用五点法求出节点上的近似导数值。请帮忙给出正确答案和分析，谢谢！
设f(χ)＝sinχ的函数表如下： 设f(χ)＝In(1＋χ)的函数表如下： (1)试用四次Newt
设f(χ)＝sinχ的函数表如下： 设f(χ)＝In(1＋χ)的函数表如下： (1)试用四次Newton插值公式计算设f(χ)＝In(1＋χ)的函数表如下： (1)试用四次New
试分别用n＝8的复化梯形公式和n＝2的复化Simpson公式计算下列定积分 并估计误差。 请帮忙给出
试分别用n＝8的复化梯形公式和n＝2的复化Simpson公式计算下列定积分，并估计误差。 请帮忙给出正确答案和分析，谢谢！
试用改进的Euler方法 计算定积分y(χ)＝用差分法求解下述边值问题的数值解用差分法求解下述边值问
试用改进的Euler方法，计算定积分y(χ)＝用差分法求解下述边值问题的数值解用差分法求解下述边值问题的数值解 请帮忙给出正确答案和分析，谢谢！
设定积分试用Romberg外推算法计算定积分(ε＝×10－5)： (1)I＝sinχdχ (2)I＝
设定积分试用Romberg外推算法计算定积分(ε＝×10－5)： (1)I＝sinχdχ (2)I＝dχ试用Romberg外推算法计算定积分(ε＝×10-5)： (1)I＝sinχdχ (2)
