设f(χ)∈C2[a b] L1(χ)是f(χ)在[a b]上的线性插值函数 证明： 并举一例 指
设f(χ)∈C2[a，b]，L1(χ)是f(χ)在[a，b]上的线性插值函数，证明：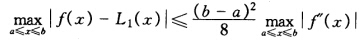 
并举一例，指出上述不等式等号可以成立。又若f(a)＝f(b)＝0，则有何结论?
请帮忙给出正确答案和分析，谢谢！
参考解答
481***102
2024-11-17 07:24:08
正确答案：由Lagrange插值余式知： R(χ)＝f(χ)－L1(χ)＝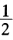
(χ－a)(χ－b)f〞(ξ) (a＜ξ＜b) 所以
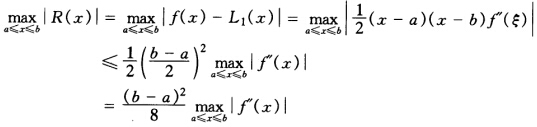例如f(χ)＝χ2L1(χ)＝a2＋(b＋a)(χ－a)R(χ)＝χ2[a2＋(b＋a)(χ－a)由R′(χ)＝0得χ＝
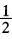(a＋b)于是R(χ)在χ＝
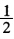(a＋b)处取得最大值即
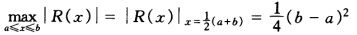又因为f〞(χ)＝2故有
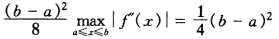所以等号成立。 若f(a)＝f(b)＝0则L1(χ)＝0也有等式成立即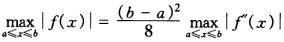
由Lagrange插值余式知：R(χ)＝f(χ)－L1(χ)＝(χ－a)(χ－b)f〞(ξ)(a＜ξ＜b)所以例如f(χ)＝χ2,L1(χ)＝a2＋(b＋a)(χ－a),R(χ)＝χ2[a2＋(b＋a)(χ－a),由R′(χ)＝0,得χ＝(a＋b),于是R(χ)在χ＝(a＋b)处取得最大值,即又因为f〞(χ)＝2,故有所以等号成立。若f(a)＝f(b)＝0,则L1(χ)＝0,也有等式成立,即
相似问题
设f(χ)＝sinχ的函数表如下： 已知函数y＝f(χ)的函数表如下： 试分别用待定系数法和带重节点
设f(χ)＝sinχ的函数表如下： 已知函数y＝f(χ)的函数表如下： 试分别用待定系数法和带重节点已知函数y＝f(χ)的函数表如下： 试分别用待定系数法
设函数f(χ)＝ 根据在节点χ＝100 101 102 103 104 105处的函数值 用五点法求
设函数f(χ)＝，根据在节点χ＝100，101，102，103，104，105处的函数值，用五点法求出节点上的近似导数值。请帮忙给出正确答案和分析，谢谢！
设f(χ)＝sinχ的函数表如下： 设f(χ)＝In(1＋χ)的函数表如下： (1)试用四次Newt
设f(χ)＝sinχ的函数表如下： 设f(χ)＝In(1＋χ)的函数表如下： (1)试用四次Newton插值公式计算设f(χ)＝In(1＋χ)的函数表如下： (1)试用四次New
试分别用n＝8的复化梯形公式和n＝2的复化Simpson公式计算下列定积分 并估计误差。 请帮忙给出
试分别用n＝8的复化梯形公式和n＝2的复化Simpson公式计算下列定积分，并估计误差。 请帮忙给出正确答案和分析，谢谢！
试用改进的Euler方法 计算定积分y(χ)＝用差分法求解下述边值问题的数值解用差分法求解下述边值问
试用改进的Euler方法，计算定积分y(χ)＝用差分法求解下述边值问题的数值解用差分法求解下述边值问题的数值解 请帮忙给出正确答案和分析，谢谢！
