min x12+x22 s．t． x2=1；请帮忙给出正确答案和分析 谢谢！
min x12+x22 s．t． x2=1；
请帮忙给出正确答案和分析，谢谢！
参考解答
456***101
2024-11-14 14:41:55
正确答案：记f(x)=x12+x22h(x)=x2-1定义罚函数 F(xσ)=f(x)+σh2(x)=x12+x22+σ(x2—1)2 σ＞0很大．令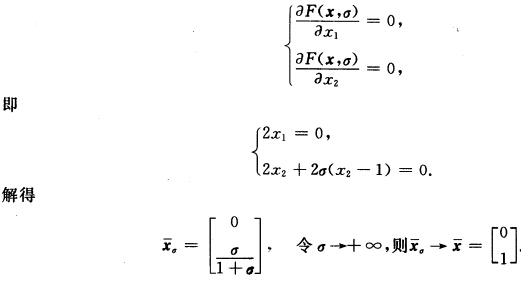
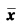为最优解最优值fmin=1．
记f(x)=x12+x22,h(x)=x2-1,定义罚函数F(x,σ)=f(x)+σh2(x)=x12+x22+σ(x2—1)2,σ＞0,很大．令为最优解,最优值fmin=1．
相似问题
设函数f(x)在x(1)与x(2)之间存在极小点 又知 f1=f(x(1)) f2=f(x(2))
设函数f(x)在x(1)与x(2)之间存在极小点，又知 f1=f(x(1))，f2=f(x(2))，f1=f’(x(1))．作二次插值多项式φ(x)，使 φ(x(1))=f1， φ(x(2))=f2， φ’
定义算法映射如下： 在集合X=[0 1]上定义算法映射 讨论在以下各点处A是否为闭的：在集合X=[0
定义算法映射如下： 在集合X=[0，1]上定义算法映射 讨论在以下各点处A是否为闭的：在集合X=[0，1]上定义算法映射 讨论在以下各点处A是否为闭的：
给定函数 用K—T条件求解下列问题 min x12一x2—3x3 s．t． 一x1一x2一x3≥0
给定函数 用K—T条件求解下列问题 min x12一x2—3x3 s．t． 一x1一x2一x3≥0， x12＋用K—T条件求解下列问题 min x12一x2—3x3 s．t． 一x1一x
假设有一个路网如下图所示 图中数字表示该路段的长度 求从A到E的最短路线及其长度． max 2x12
假设有一个路网如下图所示，图中数字表示该路段的长度，求从A到E的最短路线及其长度． max 2x12+3x2+5x3 s．t． 2x1+4x2+x3=8， x1，x2，x3≥0；请
用Frank—Wolfe方法求解下列问题：min x12＋2x22－x1x2＋4x2＋4 s．t．
用Frank—Wolfe方法求解下列问题：min x12＋2x22－x1x2＋4x2＋4 s．t． x1＋x2＋x3=5， x1，x2，x3min x12+2x22-x1x2+4x2+4 s．t． x1+x2+x3=5，
