求函数求函数f(t)=cos ω0t的傅氏变换．求函数f(t)=cos ω0t的傅氏变换．请帮忙给出
求函数求函数f(t)=cos ω0t的傅氏变换．
求函数f(t)=cos ω0t的傅氏变换．
请帮忙给出正确答案和分析，谢谢！
参考解答
456***101
2024-11-14 16:55:33
正确答案：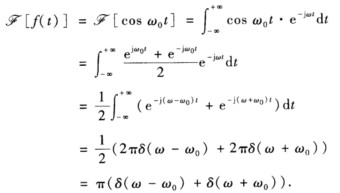
运用性质求傅氏变换和傅氏逆变换需要熟记傅氏变换的性质和一些常见函数的傅氏变换．对于一般函数则以这些常见函数及其傅氏变换为“基函数”来进行性质的“叠加”．
运用性质求傅氏变换和傅氏逆变换,需要熟记傅氏变换的性质和一些常见函数的傅氏变换．对于一般函数则以这些常见函数及其傅氏变换为“基函数”,来进行性质的“叠加”．
相似问题
计算积分计算积分其中C为： (1)连接原点O与点1＋i的直线段； (2)正向圆周|z|=2．计算积分
计算积分计算积分其中C为： (1)连接原点O与点1＋i的直线段； (2)正向圆周|z|=2．计算积分其中C为： (1)连接原点O与点1+i的直线段； (2)正向圆周|z|=2
给定原始的线性规划问题 min cx s．t． Ax=b x≥0． 假设这个问题与其对偶问题是可行
给定原始的线性规划问题 min cx s．t． Ax=b， x≥0． 假设这个问题与其对偶问题是可行的．令w(0)是对偶问题的一个已知的最优解． (1)若用μ≠0乘
考虑下列问题： min —x1—3x2 s．t． x1+x2≤6 一x1+2x2≤6 x1 x2
考虑下列问题： min —x1—3x2 s．t． x1+x2≤6， 一x1+2x2≤6， x1，x2≥0． (1)用单纯形方法求出最优解． (2)将约束右端，λ≥0，求含参数线性
解下列线性规划问题： (1)min 5x1—6x2 S．t． x1+2x2≤10 2x1一x2≤5
解下列线性规划问题： (1)min 5x1—6x2 S．t． x1+2x2≤10， 2x1一x2≤5， x1—4x2≤4， x1，x2≥0． (2)min —x1+x2 S．t． 3x1—7x2≥8，
假设一个线性规划问题存在有限的最小值f0现在用单纯形方法求它的最优解(最小值点) 设在第k次迭代得到
假设一个线性规划问题存在有限的最小值f0现在用单纯形方法求它的最优解(最小值点)，设在第k次迭代得到一个退化的基本可行解，且只有一个基变量为零(xi=0)
