求一正交变换x=Qy 将二次型f(x1 x2 x3)=x12+4x22+4x32-4x1x3+4x2
求一正交变换x=Qy，将二次型f(x1，x2，x3)=x12+4x22+4x32-4x1x3+4x2x3-8x2x3化为标准形。
请帮忙给出正确答案和分析，谢谢！
参考解答
456***101
2024-11-13 01:19:33
正确答案：二次型的矩阵为
令|A-λE|=0即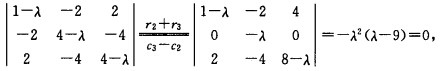
则可得A的特征值为λ1=λ2=0λ3=9。当λ1=λ2=0时解齐次线性方程组(A-0E)x=0可得特征向量
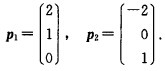将p1p2正交化取
当λ3=9时解齐次线性方程组(A-9E)x=0可得特征向量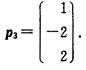
将β1β2β3单位化可得
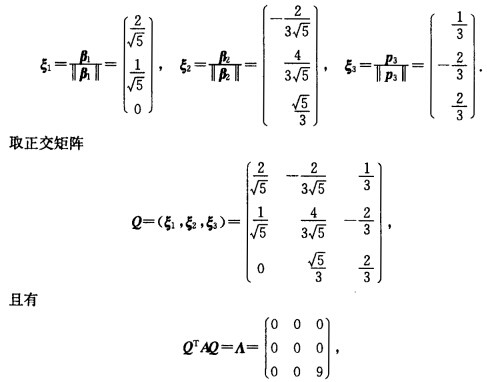则在正交变换x=Qy下将二次型化为标准形
二次型的矩阵为,令|A-λE|=0,即则可得A的特征值为λ1=λ2=0,λ3=9。当λ1=λ2=0时,解齐次线性方程组(A-0E)x=0,可得特征向量将p1,p2正交化,取当λ3=9时,解齐次线性方程组(A-9E)x=0,可得特征向量将β1,β2,β3单位化可得则在正交变换x=Qy下,将二次型化为标准形
相似问题
已知向量空间R3的两个基： 且由(1)到(2)的过渡矩阵为P= 求n b c x y z。请帮忙给
已知向量空间R3的两个基： 且由(1)到(2)的过渡矩阵为P=，求n，b，c，x，y，z。请帮忙给出正确答案和分析，谢谢！
若向量组α1 α2 α3中任何两个向量都线性无关 是否一定有α1 α2 α3线性无关?请帮忙给出正确
若向量组α1，α2，α3中任何两个向量都线性无关，是否一定有α1，α2，α3线性无关?请帮忙给出正确答案和分析，谢谢！
求矩阵A=设A=为正定矩阵 求α的取值范围。设A=为正定矩阵 求α的取值范围。请帮忙给出正确答案和分
求矩阵A=设A=为正定矩阵，求α的取值范围。设A=为正定矩阵，求α的取值范围。请帮忙给出正确答案和分析，谢谢！
设A B为n阶矩阵 当A可逆时 证明AB与BA具有相同的特征值的性质。请帮忙给出正确答案和分析 谢谢
设A、B为n阶矩阵，当A可逆时，证明AB与BA具有相同的特征值的性质。请帮忙给出正确答案和分析，谢谢！
设A是3阶方阵 且|A|=2 求 下列做法是否正确? 此题为判断题(对 错)。请帮忙给出正确答案和
设A是3阶方阵，且|A|=2，求 下列做法是否正确? 此题为判断题(对，错)。请帮忙给出正确答案和分析，谢谢！
