参考解答
正确答案:不唯一。因为二次型对应的矩阵对角化后的对角矩阵不唯一导致二次型的标准形不唯一。例如(x1x2x3)=2x1x2+2x1x3+2x2x3若采取正交变换法则有(1)取正交矩阵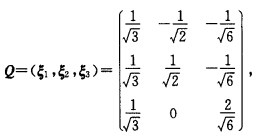 在正交变换x=Qy下将二次型化为标准型
在正交变换x=Qy下将二次型化为标准型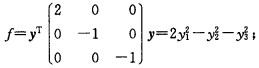 (2)取正交矩阵
(2)取正交矩阵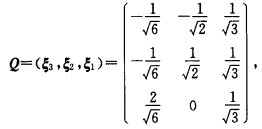 在正交变换x=Qy下将二次型化为标准型
在正交变换x=Qy下将二次型化为标准型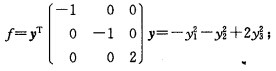 若采取配方法令x=Pz。其中
若采取配方法令x=Pz。其中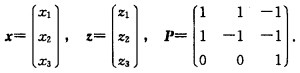 在上述可逆变换下可将该二次型化为标准形
在上述可逆变换下可将该二次型化为标准形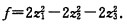 可见二次型的标准型并不唯一。
可见二次型的标准型并不唯一。
不唯一。因为二次型对应的矩阵对角化后的对角矩阵不唯一,导致二次型的标准形不唯一。例如,(x1,x2,x3)=2x1x2+2x1x3+2x2x3,若采取正交变换法,则有(1)取正交矩阵在正交变换x=Qy下,将二次型化为标准型(2)取正交矩阵在正交变换x=Qy下,将二次型化为标准型若采取配方法,令x=Pz。其中在上述可逆变换下,可将该二次型化为标准形可见二次型的标准型并不唯一。
相似问题
是否所有的n阶方阵都一定能对角化?请帮忙给出正确答案和分析 谢谢!
是否所有的n阶方阵都一定能对角化?请帮忙给出正确答案和分析,谢谢!
证明向量组a1=构成R3的一个基 并求向量在这个基下的坐标。请帮忙给出正确答案和分析 谢谢!
证明向量组a1=构成R3的一个基,并求向量在这个基下的坐标。请帮忙给出正确答案和分析,谢谢!
下面计算是否正确?若不正确 请加以改正。 此题为判断题(对 错)。请帮忙给出正确答案和分析 谢谢!
下面计算是否正确?若不正确,请加以改正。 此题为判断题(对,错)。请帮忙给出正确答案和分析,谢谢!
若A可对角化 即存在相似变换矩阵P 使得P-1AP=A为对角矩阵 问此过程中的相似变换矩阵P是否唯一
若A可对角化,即存在相似变换矩阵P,使得P-1AP=A为对角矩阵,问此过程中的相似变换矩阵P是否唯一,A是否唯一?请帮忙给出正确答案和分析,谢谢!
若矩阵A与B相似 试证:R(A)=R(B)。R(A)=R(B)。请帮忙给出正确答案和分析 谢谢!
若矩阵A与B相似,试证:R(A)=R(B)。R(A)=R(B)。请帮忙给出正确答案和分析,谢谢!












