证明向量组a1=构成R3的一个基 并求向量在这个基下的坐标。请帮忙给出正确答案和分析 谢谢！
证明向量组a1=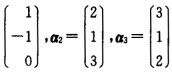
构成R3的一个基，并求向量
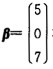在这个基下的坐标。
请帮忙给出正确答案和分析，谢谢！
参考解答
490***101
2024-11-12 23:46:26
正确答案：由于A=(α1α2α3)=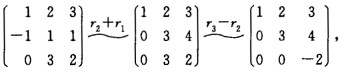
则R(A)=3。从而α1α2α3线性无关故构成R3的一个基。设β在基α1α2α3下的坐标向量为x即β=(α1α2α3)x则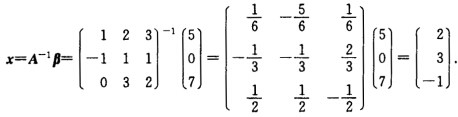
由于A=(α1,α2,α3)=则R(A)=3。从而α1,α2,α3线性无关,故构成R3的一个基。设β在基α1,α2,α3下的坐标向量为x,即β=(α1,α2,α3)x,则
相似问题
下面计算是否正确?若不正确 请加以改正。 此题为判断题(对 错)。请帮忙给出正确答案和分析 谢谢！
下面计算是否正确?若不正确，请加以改正。 此题为判断题(对，错)。请帮忙给出正确答案和分析，谢谢！
若A可对角化 即存在相似变换矩阵P 使得P-1AP=A为对角矩阵 问此过程中的相似变换矩阵P是否唯一
若A可对角化，即存在相似变换矩阵P，使得P-1AP=A为对角矩阵，问此过程中的相似变换矩阵P是否唯一，A是否唯一?请帮忙给出正确答案和分析，谢谢！
若矩阵A与B相似 试证：R(A)=R(B)。R(A)=R(B)。请帮忙给出正确答案和分析 谢谢！
若矩阵A与B相似，试证：R(A)=R(B)。R(A)=R(B)。请帮忙给出正确答案和分析，谢谢！
请用矩阵的形式表示： (1)线性方程a1x1＋a2x2＋…＋anxn=b； (2)线性方程组 设矩阵
请用矩阵的形式表示： (1)线性方程a1x1＋a2x2＋…＋anxn=b； (2)线性方程组 设矩阵A为n阶方阵，则下设矩阵A为n阶方阵，则下述说法之间的关系如何? (1
设A为n阶方阵 A*为其伴随矩阵 k为非零实数 证明 (kA)*=kn-1A*。请帮忙给出正确答案和
设A为n阶方阵，A*为其伴随矩阵，k为非零实数，证明 (kA)*=kn-1A*。请帮忙给出正确答案和分析，谢谢！
