判断下列复级数的敛散性 若收敛指明条件收敛还是绝对收敛． 判断下列级数的敛 散性．判断下列级数的敛
判断下列复级数的敛散性，若收敛指明条件收敛还是绝对收敛． 判断下列级数的敛、散性．
判断下列级数的敛、散性．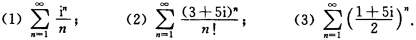 
请帮忙给出正确答案和分析，谢谢！
参考解答
456***103
2024-11-21 13:44:56
正确答案：(1)因为i2=一1i3=一1i4=1…i1=i所以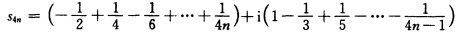
利用交错级数收敛性判别法及极限运算法则知
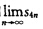存在．设为l此外显然有
(1)因为i2=一1,i3=一1,i4=1,…,i1=i,所以利用交错级数收敛性判别法及极限运算法则知存在．设为l,此外,显然有
相似问题
设函数f(z)在区域D内解析 试证 ｜f(z)｜2=4｜f(z)｜2．请帮忙给出正确答案和分析 谢谢
设函数f(z)在区域D内解析，试证 ｜f(z)｜2=4｜f(z)｜2．请帮忙给出正确答案和分析，谢谢！
若f(z)在圆｜z｜＜R内解析 f(0)=0 ｜f(z)｜≤M＜＋∞ 则 (1)｜f(z)｜≤试在原
若f(z)在圆｜z｜＜R内解析，f(0)=0，｜f(z)｜≤M＜＋∞，则 (1)｜f(z)｜≤试在原点去心邻域内把函数f(z)=展开成试在原点去心邻域内把函数f(z)=展开成洛
设在区域D={z｜｜arg z｜＜}内的单位圆周｜z｜=1上任取一点z 用D内曲线C连接0与z 试证
设在区域D={z｜｜arg z｜＜}内的单位圆周｜z｜=1上任取一点z，用D内曲线C连接0与z，试证 请帮忙给出正确答案和分析，谢谢！
求证下列不等式： (1)利用积分估值 证明 (1)｜∫C(x2＋iy2)dz｜≤2 其中C是连接一i
求证下列不等式： (1)利用积分估值，证明 (1)｜∫C(x2＋iy2)dz｜≤2，其中C是连接一i到i的直线段； 利用积分估值，证明 (1)｜∫C(x2+iy2)dz｜≤2，其
设f(z)= 试证f(z)在原点满足C一R方程 但却不可微．请帮忙给出正确答案和分析 谢谢！
设f(z)= 试证f(z)在原点满足C一R方程，但却不可微．请帮忙给出正确答案和分析，谢谢！
