求证下列不等式： (1)利用积分估值 证明 (1)｜∫C(x2＋iy2)dz｜≤2 其中C是连接一i
求证下列不等式： (1)利用积分估值，证明 (1)｜∫C(x2＋iy2)dz｜≤2，其中C是连接一i到i的直线段；
利用积分估值，证明 (1)｜∫C(x2+iy2)dz｜≤2，其中C是连接一i到i的直线段； (2)｜∫C(x2+iy2)dz｜≤π，其中C是连接一i到i的右半圆周．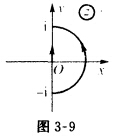 
请帮忙给出正确答案和分析，谢谢！
参考解答
456***103
2024-11-21 13:35:58
正确答案：×
(1)C：z=it,一1≤t≤1,因为｜f(z)｜=｜x2+iy2｜=｜it2｜=t2≤1,而积分路径长为｜i一(一i)｜=2．故｜(x2+iy2)dz｜≤1×2=2．(2)C：z=eθ,,而｜f(z)｜=｜x2+iy2｜=≤x2+y2=1,右半圆周长为π所以｜∫-11(x2+iy2)dz｜≤1．π=π
相似问题
设f(z)= 试证f(z)在原点满足C一R方程 但却不可微．请帮忙给出正确答案和分析 谢谢！
设f(z)= 试证f(z)在原点满足C一R方程，但却不可微．请帮忙给出正确答案和分析，谢谢！
设a b为实数 s=σ+it(σ＞0)时 试证 ｜ebs一eas｜≤｜s｜｜b一a｜emax{a b
设a，b为实数，s=σ+it(σ＞0)时，试证 ｜ebs一eas｜≤｜s｜｜b一a｜emax{a,b} σ．请帮忙给出正确答案和分析，谢谢！
设函数f(z)在｜z｜＜1内解析 在闭圆｜z｜≤1上连续 且f(0)=1 求积分 之值．请帮忙给出
设函数f(z)在｜z｜＜1内解析，在闭圆｜z｜≤1上连续，且f(0)=1，求积分 之值．请帮忙给出正确答案和分析，谢谢！
设f(z)是一个整函数 且假定存在着一个非负整数n 以及两个正数R与M 使当｜z｜≥R时 ｜f(z)
设f(z)是一个整函数，且假定存在着一个非负整数n，以及两个正数R与M，使当｜z｜≥R时，｜f(z)｜≤M｜z｜n。请帮忙给出正确答案和分析，谢谢！
试解方程： (1)ez=； (3)1+ez=0； (4)cos z+sin z=0； (5)tan
试解方程： (1)ez=； (3)1+ez=0； (4)cos z+sin z=0； (5)tan z=1+2i．请帮忙给出正确答案和分析，谢谢！
