试解方程: (1)ez=; (3)1+ez=0; (4)cos z+sin z=0; (5)tan
试解方程: (1)ez=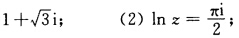 ; (3)1+ez=0; (4)cos z+sin z=0; (5)tan z=1+2i.
; (3)1+ez=0; (4)cos z+sin z=0; (5)tan z=1+2i.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案: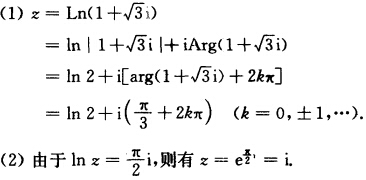 (3)由ez=一1得z=Ln(一1)=i(π+2kπ)k∈Z.(4)由cos z=一sin z即tan z=一1所以
(3)由ez=一1得z=Ln(一1)=i(π+2kπ)k∈Z.(4)由cos z=一sin z即tan z=一1所以
(3)由ez=一1,得z=Ln(一1)=i(π+2kπ),k∈Z.(4)由cosz=一sinz,即tanz=一1,所以
相似问题
求证下列不等式: (1)为连结点一i到i的直线段. (2)|∫eeizdz|<π 其中C为圆周|z|
求证下列不等式: (1)为连结点一i到i的直线段. (2)|∫eeizdz|<π,其中C为圆周|z|=R的上半圆周从R到一R.请帮忙给出正确答案和分析,谢谢!
设(1)区域D是有界区域 其边界是周线或复周线C;(2)函数f1(z)及f2(z)在D内解析 在闭域
设(1)区域D是有界区域,其边界是周线或复周线C;(2)函数f1(z)及f2(z)在D内解析,在闭域=D+C上连续;(3)沿C,f1(z)=f2(z),试证:在整个闭域D上,f1(z)≡f
设z=x+iy 试求 (1)|ei-2z|; (2)试求下面各式之值: (1)e3+i; (2)co
设z=x+iy,试求 (1)|ei-2z|; (2)试求下面各式之值: (1)e3+i; (2)cos(1一i).试求下面各式之值: (1)e3+i; (2)cos(1一i).请帮忙给出正确答案和分析,谢谢!
试解方程: (1)ez=(形式导数)(1)设二元实变函数u(x y)有偏导数 此函数可以写成z=x+
试解方程: (1)ez=(形式导数)(1)设二元实变函数u(x,y)有偏导数,此函数可以写成z=x+iy及的函数 (形式导数)(1)设二元实变函数u(x,y)有偏导数,此函数
设(1)区域D含有实轴的一段L; (2)函数u(x y)+iv(x y)及 u(z 0)+iv(z
设(1)区域D含有实轴的一段L; (2)函数u(x,y)+iv(x,y)及 u(z,0)+iv(z,0) (z=x+iy) 都在区域D内解析,则(试证)在D内 u(x,y)+iv(x,y)≡u(z,0)+i












