试用n=1 2 3 4的Newton-cotes求积公式计算定积分I=试用复化Simpson公式计算
试用n=1,2,3,4的Newton-cotes求积公式计算定积分I=试用复化Simpson公式计算积分I=∫123lnχdχ要求
试用复化Simpson公式计算积分I=∫123lnχdχ要求截断误差不超过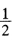 ×10-5,并把计算结果与准确值比较。
×10-5,并把计算结果与准确值比较。
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:×
由复化Simpson截断误差有|Rs[f,h|=而f(χ)=3lnχ,f4(χ)==18要想|Rs[f,h|≤×10-5则要h<×10-1=5.95,故n≥6,于是取n=6,h=得而I=∫123lnχdχ=(3χlnχ-χ)|12=1.15888308故误差估计为|Rs[f,h|≤1.02×10-6
相似问题
设线性方程组 证明:用Jacobi迭代法和Gauss-Seidel迭代法求解方程组均收敛。取初始解向
设线性方程组 证明:用Jacobi迭代法和Gauss-Seidel迭代法求解方程组均收敛。取初始解向量χ(0)=[0,0,0]T,分别用上逮两种方法求解(ε)=×10-5,并比
设f(χ)=sinχ的函数表如下: 设函数y=sinχ的函数表如下: 试用等距节点Newton后插公
设f(χ)=sinχ的函数表如下: 设函数y=sinχ的函数表如下: 试用等距节点Newton后插公式,计算设函数y=sinχ的函数表如下: 试用等距节点Newton后
设隐式单步法公式 yn+1=yn+[4f(χn yn)+2f(χn+1 yn+1)+hf′(χn y
设隐式单步法公式 yn+1=yn+[4f(χn,yn)+2f(χn+1,yn+1)+hf′(χn,yn)] 证明:它是三阶方法。请帮忙给出正确答案和分析,谢谢!
设初值问题应用Adams预估一校正方法解初值问题 取h=0.1计算其数值解 并与精确解比较。应用Ad
设初值问题应用Adams预估一校正方法解初值问题 取h=0.1计算其数值解,并与精确解比较。应用Adams预估一校正方法解初值问题 取h=0.1计算其数值解
设χ∈Rn (1)‖χ‖∞≤‖χ‖1≤n‖χ‖∞; (2)‖χ‖∞≤‖χ‖2≤设线性方程组 已知一
设χ∈Rn, (1)‖χ‖∞≤‖χ‖1≤n‖χ‖∞; (2)‖χ‖∞≤‖χ‖2≤设线性方程组 已知一个近似解χ(0)=(-设线性方程组 已知一个近似解χ(0)=(












